Optimisez le dimensionnement et calculez automatiquement l'acier et le ferraillage nécessaires pour vos poutres en béton armé (poutres isostatiques rectangulaires en flexion simple) grâce à notre logiciel libre et open source, conforme à l’Eurocode 2 (NF EN 1992-1-1).
Distribué sous licence MIT, il simplifie le processus de calcul, garantit des résultats précis et favorise la réutilisation et l’interopérabilité des données. Il s’inscrit dans une démarche européenne de logiciels libres pour l’ingénierie, contribuant à la transparence, à la collaboration et à la création d’un patrimoine numérique commun.
Le code source complet est disponible sur GitHub, permettant à chacun de l’auditer, de l’améliorer ou de l’adapter à ses besoins. Cette ouverture contribue au bien commun en rendant accessibles à tous les méthodes de calcul normalisées, tout en respectant les standards européens.
Notre calculateur offre une solution pratique et fiable pour les ingénieurs, étudiants en génie civil, architectes et passionnés de construction. Il permet de déterminer rapidement les dimensions des poutres en fonction des charges appliquées et des propriétés du béton, de calculer les sections d'acier nécessaires, de vérifier les contraintes et moments fléchissants, et de sélectionner automatiquement les diamètres et quantités de barres normalisées en Europe. Il dispose automatiquement l'acier calculé dans la poutre et génère la répartition des cadres, étriers ou épingles selon l’EC2.
Le logiciel inclut également le calcul automatique des arrêts de barres, des longueurs d’ancrage, du diamètre de mandrin et des retours de façonnage conformément à l’Eurocode 2. Les résultats sont exportables en PDF et exploitables dans d’autres outils grâce à un format de données interopérable, favorisant la réutilisation dans des workflows BIM ou des logiciels de calcul tiers.
Important : cet outil fournit des résultats préliminaires. Une vérification par un bureau d’études en béton armé agréé reste indispensable avant toute mise en œuvre réelle.
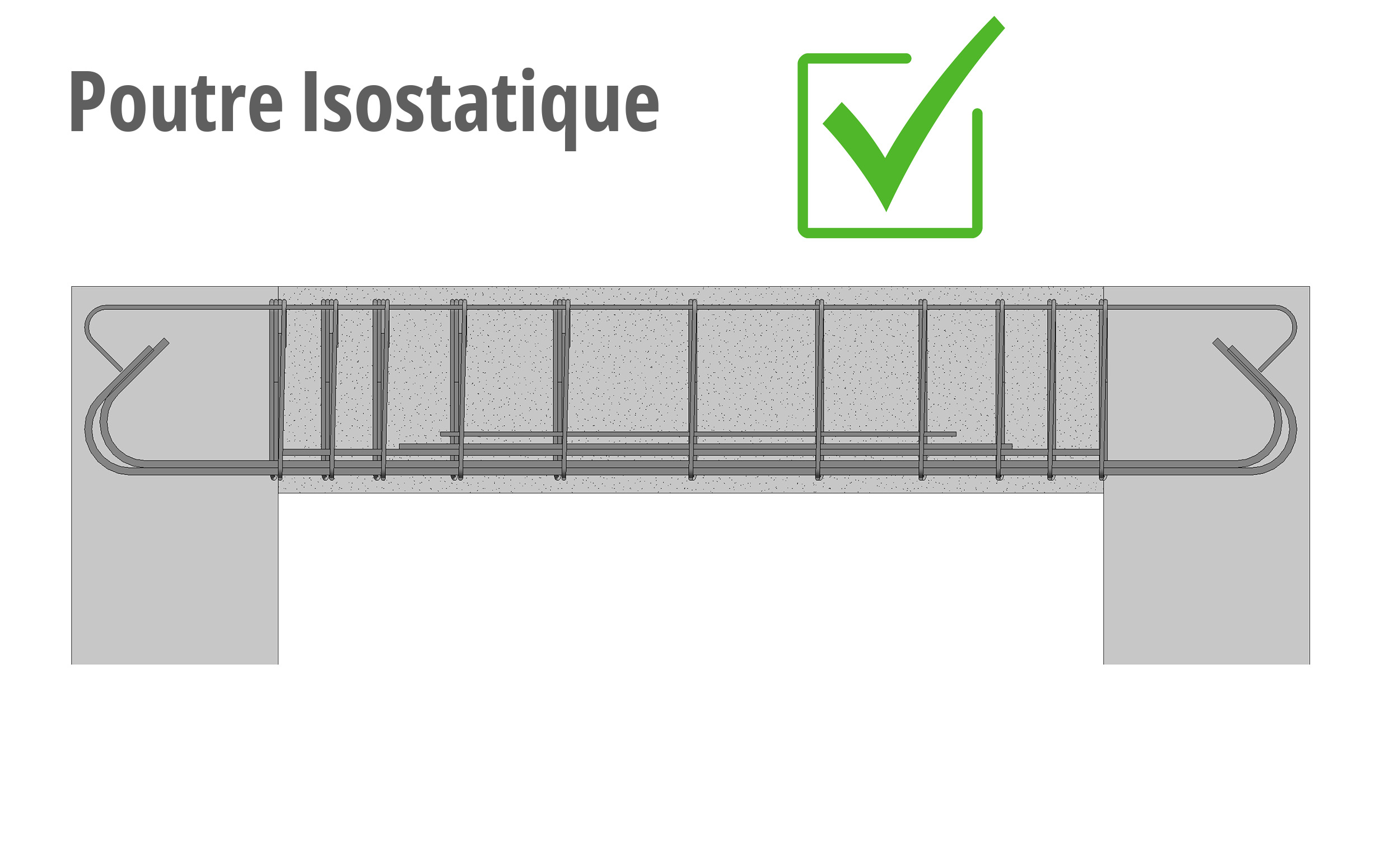
Cet outil est spécifiquement conçu pour le calcul des poutres isostatiques rectangulaires en flexion simple, conformément aux prescriptions de l’Eurocode 2.
Appuyées sur deux simples appuis, sans charges ou conditions supplémentaires modifiant la répartition des efforts.
Soumises à des charges perpendiculaires à leur longueur, provoquant une flexion, avec une section de forme rectangulaire.
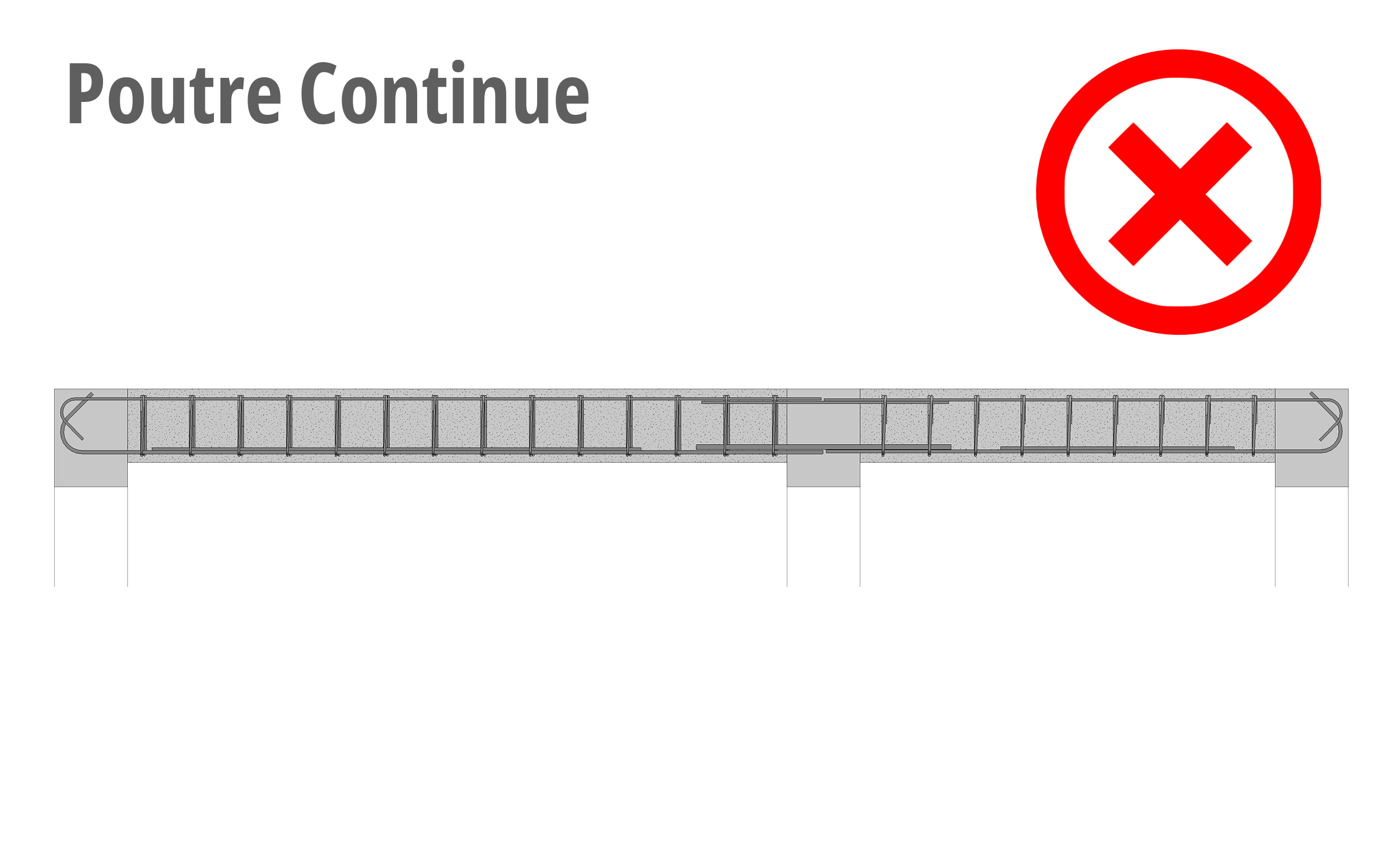
Note importante : non adapté aux poutres continues ou à géométrie complexe.
Responsabilité : Les calculs sont préliminaires et doivent être validés par un bureau d’études agréé. Les auteurs déclinent toute responsabilité en cas d’utilisation inappropriée.
Sélectionnez les paramètres préliminaires de votre projet de construction dans le tableau ci-dessous.
Vous pourrez corriger toutes les valeurs ultérieurement.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
La durée d’utilisation :
T
Ans
Acier à béton :
B
MPa
Coefficient réducteur pour les actions variables :
Ψ2
-
Enrobage minimal pour une bonne adhérence:
cmin,b
mm
cmin,b = ∅ de la barre ou ∅ des plus gros granulats (ajustez cette valeur en fonction des résultats obtenus).
Enrobage minimal :
cmin = max [cmin,b ; cmin,dur ; 10 mm]
mm
Enrobage nominal à respecter :
cnom = cmin + Δcdev
m
Enrobage réel:
c
m
Dimension nominale du plus gros granulat:
Dmax
mm
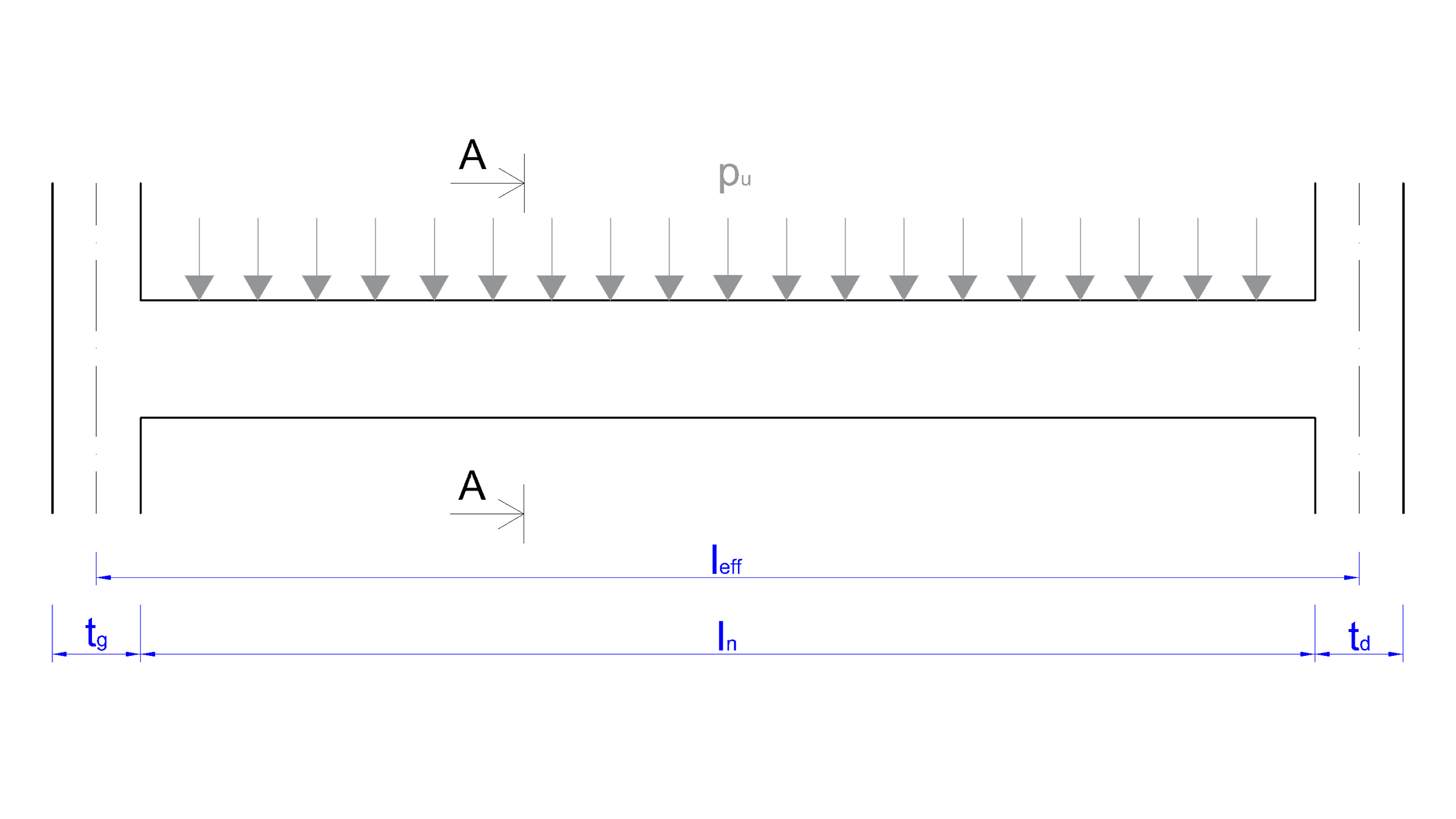
Pour un dimensionnement préliminaire de votre poutre en béton armé, conformément à l’Eurocode 2 (NF EN 1992-1-1), référez-vous aux schémas ci-dessous. Toutes les dimensions peuvent être modifiées ultérieurement en fonction des résultats obtenus.
Pour déterminer la hauteur utile de la section "d", utilisez le résultat anticipé danticipé = (0.9 × h) indiqué dans la colonne "Remarques". Ajustez cette valeur après calcul, en fonction de la hauteur utile réelle dréel obtenue dans le tableau Disposition des aciers longitudinaux, pour plus de précision.
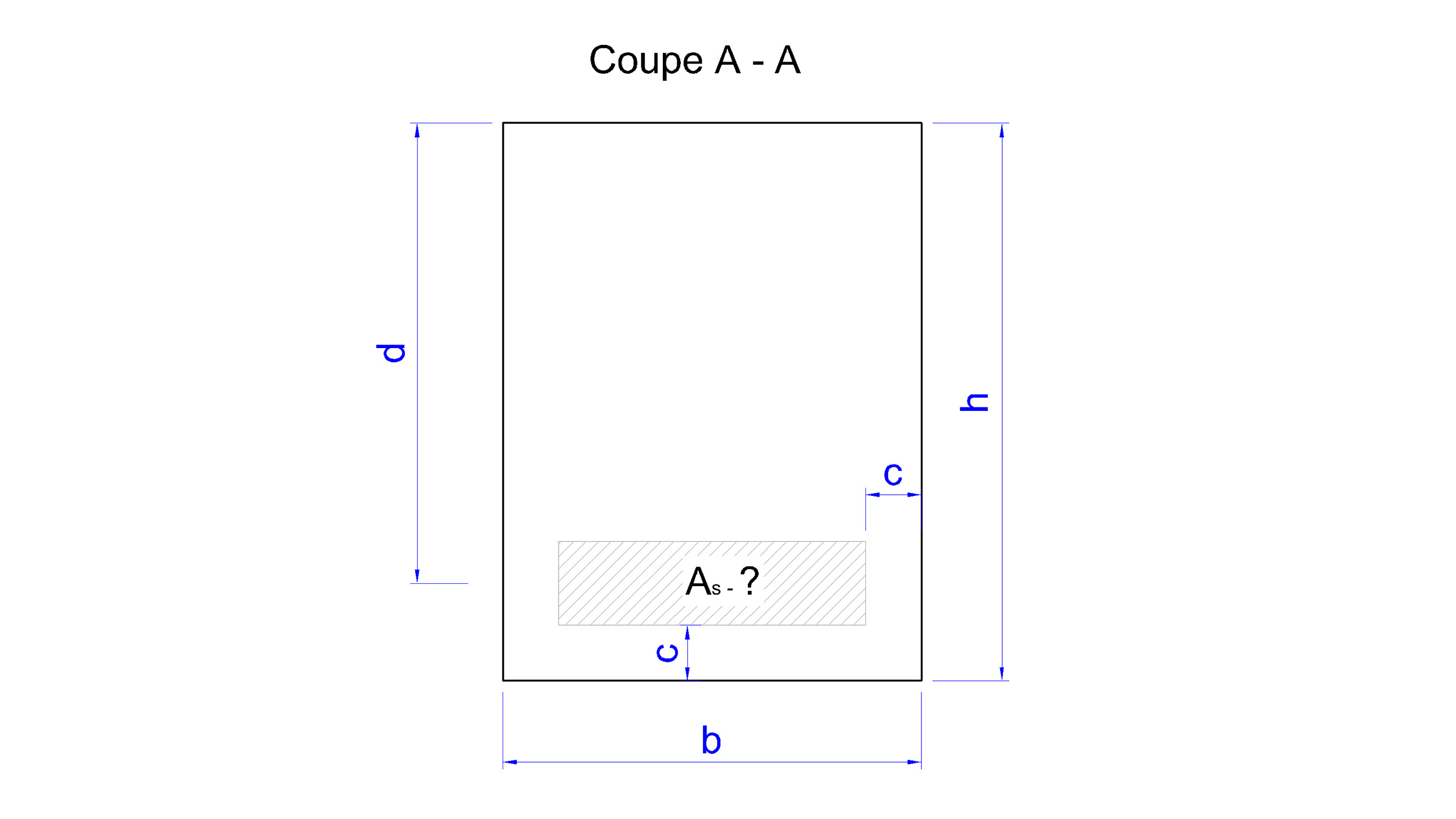
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Largeur de la poutre :
b
m
Hauteur de la poutre :
h
m
La portée entre nus des appuis :
ln
m
Largeur d'appui gauche :
tg
m
Largeur d'appui droit :
td
m
La portée entre axes :
leff
m
La hauteur utile de la section :
d = h - (enrobage + ∅/2)
m
danticipé = (0.9 x h), (ajustez cette valeur en fonction des résultats obtenus.)
Distance du centre de gravité des armatures comprimées :
c' = enrobage + ∅'/2
m
Généralement entre 0,03 et 0,07 m, (ajustez cette valeur en fonction des résultats obtenus).
Pour dimensionner une poutre en béton armé conformément à l’Eurocode 2, renseignez les valeurs suivantes :
Ces valeurs doivent provenir d’un calcul de descente de charges afin de refléter fidèlement les sollicitations réelles appliquées à la poutre.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Charges permanentes
(uniformément réparties par mètre de poutre) :
Gu
kN/m
Actions variables
(charges d'exploitations uniformément réparties):
Q
kN/m
Poids propre de la poutre par mètre linéaire :
Gpp = b*h*25kN/m3
kN/m
Actions permanentes :
G = Gu + Gpp
kN/m
Action totale pondérée à ELU :
pu = 1,35G + 1,5Q
kN/m
Action totale pondérée à ELS :
pser,qp = G + Ψ2Q
kN/m
Moment fléchissant maximal (ELU):
MEd = pu * leff² / 8
kNm
Moment fléchissant quasi-permanent (ELS):
Mqp = pser,qp * leff² / 8
kNm
Effort tranchant maximal de calcul (ELU):
VEd = pu * ln / 2
kN
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Resistance du beton en compression :
fck
MPa
Resistance du beton en flexion:
fcd = αcc * (fck/ɣc)
MPa
Resistance du beton en traction :
fctk, 0.05
MPa
Déformation relative en compression :
εc2 = 2x10-3 si classe < C55;
‰
Déformation relative ultime en compression :
εcu2 = 3.5x10-3 si classe < C55;
‰
Appellation
Symbole / Formule
Valeur
Unité
Remarques
La limite élastique de l’acier :
fyk
MPa
Limite élastique de calcul pour l’acier :
fyd = fyk / ɣs
MPa
Module d'élasticité :
Es
MPa
Déformation ultime de l’acier de classe B :
εuk
%
Déformation utilisable :
εud = 0.9 * εuk
%
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Moment réduit :
μ = MEd / (b * d² * fcd)
-
La hauteur relative de la zone comprimée :
α (x/d) = 1,25(1 - √(1 - 2μ))
-
Section d’acier en compression :
A'
cm²
Section d’acier en traction :
As
cm²
Vérification
Formule / Condition
Valeurs
Statut
Remarques
Taux d'armature maximal :
As ≤ As,max = 0,04Ac
Taux d'armature minimale (non-fragilité) :
As > As,min
As,min = max [0.26*(fctm/fyk)*d*b; 1.30/00*d*b]
Vérification de la contrainte de compression :
σc,qp,ser ≤ 0.45fck
σc,qp,ser = Mqp * x / I;
Vérification de la flèche simplifiée (par le rapport l/d) :
leff/d ≤ A1, si ρ ≤ ρ0
leff/d ≤ A2, si ρ > ρ0
K = 1 (travée isolée).
Le diamètre de l'acier transversal doit être adapté à la hauteur utile d de la poutre. Voici les recommandations selon l'Eurocode 2 :
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Diamètre de l'acier transversal cadre :
∅w,cad
mm
Pourcentage maximal d’ajustement de As :
%As_max
%
L'espacement maximal des armatures longitudinales :
amax
cm
Nombre min de colonnes d’acier longitudinales :
nc,min = ceil (b-2*c / st,max)
n
Distance verticale entre les lits :
a1
cm
Hauteur utile réelle de la section :
dreel
m
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Sélection du type d'armature transversale :
Épingle / Étrier
-
Diamètre de l'acier transversal épingle/étrier :
∅w,e
mm
Angle d'inclinaison des diagonales comprimées :
45° ≥ θ ≥ 22°
1 ≤ cotgθ ≤ 2.5
°
Nombre d'épingles (étriers) par cadre :
nép/étr
u
Selon le calcul des barres longitudinales.
Bras de levier interne :
z = 0.9*d
m
La composante horizontale de l'effort tranchant :
AC = z*cotgθ
m
Effort tranchant pour l'acier transversal :
VEd,AC = VEd - pu*AC
kN
Coefficient de réduction du cisaillement :
ν1 = 0,6*(1-fck/250)
kN
Résistance maximale au cisaillement :
VRd,max = αcw* (bw*z*cotgϴ/1+cotg²ϴ) *ν1*fcd
αcw = 1 - flexion simple.
kN
Section d'acier des armatures transversales :
Asw = As,brins * nbrins
cm²
Espacement minimum des aciers transversaux :
st,min = (Asw/bw) * (2*fywd/ν1*fcd)
m
Espacement maximal pour le cisaillement :
st,max,rw = (Asw/bw) * (fywk/0.08*√fck)
m
Espacement maximal des aciers transversaux :
st,max = 0.75*d
m
Espacement maximal admissible des aciers transversaux :
smax = min [st,max; st,max,rw]
m
Espacement initial calculé :
sinit_cal =(Asw/VEd,AC)*z*cotgθ*fywd
m
Espacement initial sélectionné :
sinit
m
Quantité de cadres :
ncadres
pcs
Hauteur de cadre :
hcadres
m
Largeur de cadre :
lcadres
m
Quantité des étriers/épingles :
népingles
pcs
Hauteur des étriers/épingles :
hépingles
m
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Longueur d'armature pour le cisaillement :
al = (z*cotgϴ)/2
m
Section d'acier réelle :
As,reel
cm²
Moment résistant :
MRd = (MEd/As,calcule)*As,reel
kNm
Contrainte de traction axiale de calcul :
fctd = αct * (fctk,0.05 / ɣc)
MPa
Contrainte ultime d’adhérence de calcul :
fbd = 2.25*η1*η2*fctd
MPa
Contrainte d’acier de calcul :
σsd = fyd
MPa
Enrobage de calcul pour les ancrages :
cd = min [a/2; cmin]
cm
Moment décalé sur l'appui gauche :
MEd,décalé,g = MEd,max - (pu*(Leff/2 - (tg,axe + al))²/2);
kNm
Moment décalé sur l'appui droit :
MEd,décalé,d = MEd,max - (pu*(Leff/2 - (td,axe + al))²/2);
kNm
| Lit 1 | Lit 2 | Lit 3 | Lit 4 | Lit 5 | |
|---|---|---|---|---|---|
|
𝛼1 - Ancrage droit/courbe Ancrage droit : 𝛼1 = 1 Ancrage courbe : 𝛼1 = 0.7 si cd > 3*∅ |
/ | / | / | / | / |
|
𝛼2 - Ancrage droit/courbe Ancrage droit : 𝛼2 = 1 - 0.15 * ((cd - ∅) / ∅) Ancrage courbe : 𝛼2 = 1 - 0.15 * ((cd - 3*∅) / ∅) |
/ | / | / | / | / |
| 𝛼3 | |||||
| 𝛼4 | |||||
| 𝛼5 |
| BARRES : | Lit 1 | Lit 2 | Lit 3 | Lit 4 | Lit 5 |
|---|---|---|---|---|---|
| Nombre : | |||||
| Diamètre ∅ : | |||||
| Section d'acier As : | |||||
| Moment résistant MRd : | |||||
| Ancrage sur appuis gauche: |
|||||
| Ancrage sur appuis droit: |
|||||
| Longueur des barres : | |||||
| Longueur d'ancrage de calcul requise : lb,rqd = (∅/4)*(σsd/fbd) |
|||||
| Longueur d'ancrage minimale : lb,min = max [0.3*lb,rqd; 10*∅; 100mm] |
|||||
| Longueur d'ancrage de calcul droit/courbe : lbd = α1*α2*α3*α4*α5*lb,rqd |
|||||
| Centre de gravité réel des barres Gr : | |||||
| Débord de la zone d'ancrage côté travée : Da= Gr * (cotgθ)/2 |
|||||
| Espace disponible pour ancrage d'appuis gauche : Ea,g = tg - c + Da |
|||||
| Espace disponible pour ancrage d'appuis droit : Ea,d = td - c + Da |
|||||
| Type d'ancrage à l'appui gauche : | |||||
| Type d'ancrage à l'appui droit : | |||||
| Angle de façonnage de l'ancrage courbe à l'appui gauche (en degrés) : | |||||
| Angle de façonnage de l'ancrage courbe à l'appui droit (en degrés) : | |||||
| Résistance à la traction de calcul : Fbt = π*(∅²/4)*(1/fyd) |
|||||
|
Longueur maximale du retour de l'armature après courbure : Retour ≤ 5*∅ |
|||||
| Diamètre minimal de mandrin : ∅m,min = 4*∅ - si ∅ ≤ 16 mm; ∅m,min = 7*∅ - si ∅ > 16 mm. |
|||||
| Diamètre de mandrin calculé : ∅m,calcul = Fbt*(((1/ab) + (1/2*∅))/fcd) |
|||||
|
Vérifications pour mandrin gauche / droit ∅m = ∅m,min : Vérif. 1 : lb,eq ≤ Ea; lb,eq = α1*lb,rqd; Vérif. 2 : lbd,reel ≥ lbd; lbd,reel = retour + lcourbure + (Ea - ∅m,min/2). OK : Condition satisfaite, NS : Non satisfaite, NR : Non requis. |
|||||
| Diamètre de mandrin appui gauche / droit sélectionné ∅m* : | |||||
| Longueur du retour après courbure (gauche ou droite) : |
| BARRES : | Nombre | Diametre | Mandrin g/d | Retour g/d | Remarques |
|---|---|---|---|---|---|
| Lit 1 (Haut) |
| Élément | Valeur | Unité |
|---|---|---|
|
Volume de béton (calculé sur la portée entre nus des appuis) |
0.312 | m³ |
| Masse de béton | 748.8 | kg |
| Masse d’acier | 36.1 | kg |
| Masse totale (béton + acier) | 784.9 | kg |
| Ratio acier/béton | 4.82 | % |
| Longueur totale d’armatures | 43.59 | m |
| Diamètre moyen | 14 | mm |
Disposer les barres d'armature conformément aux schémas ci-dessous, représentant la répartition longitudinale et en coupe du ferraillage pour assurer la résistance structurelle requise.
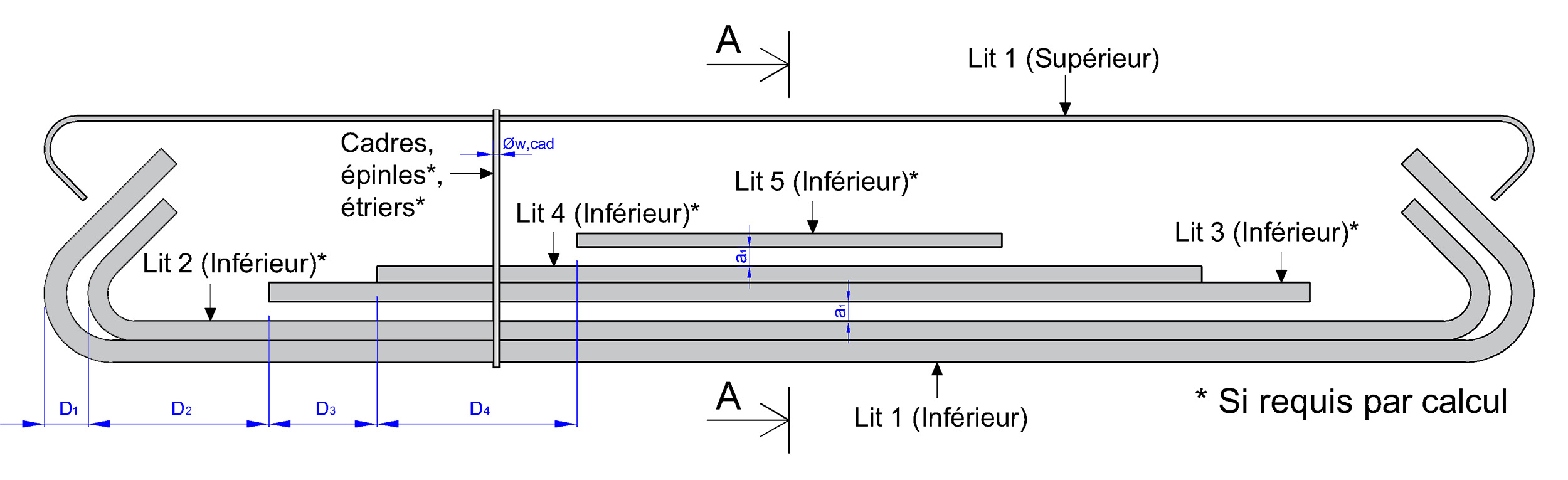
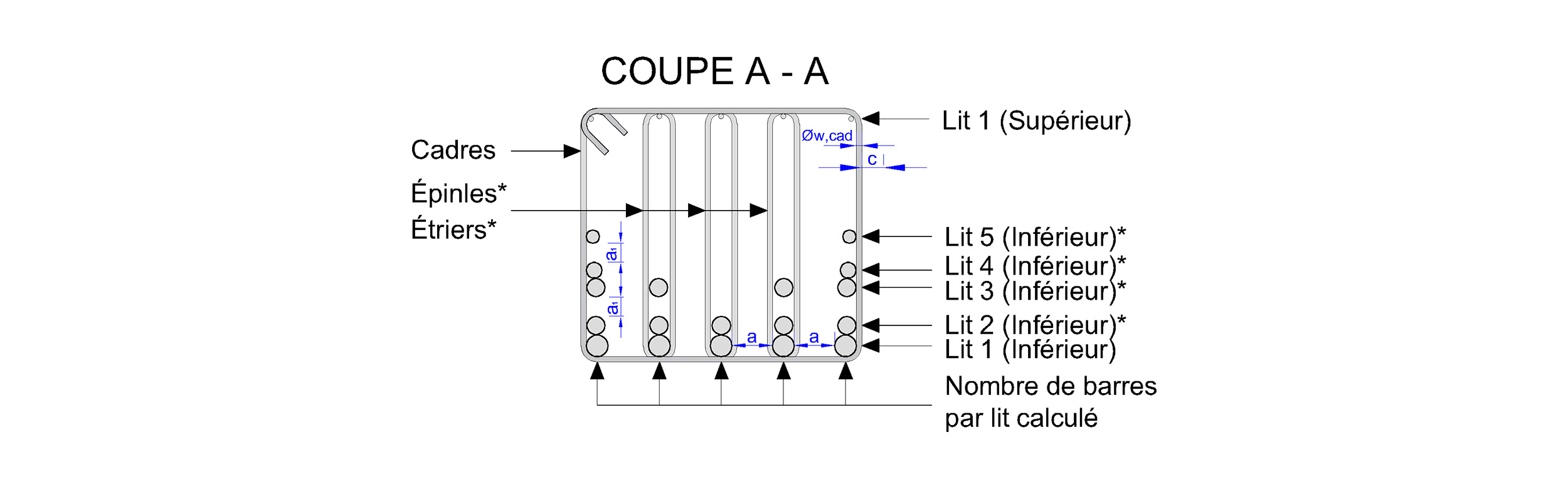
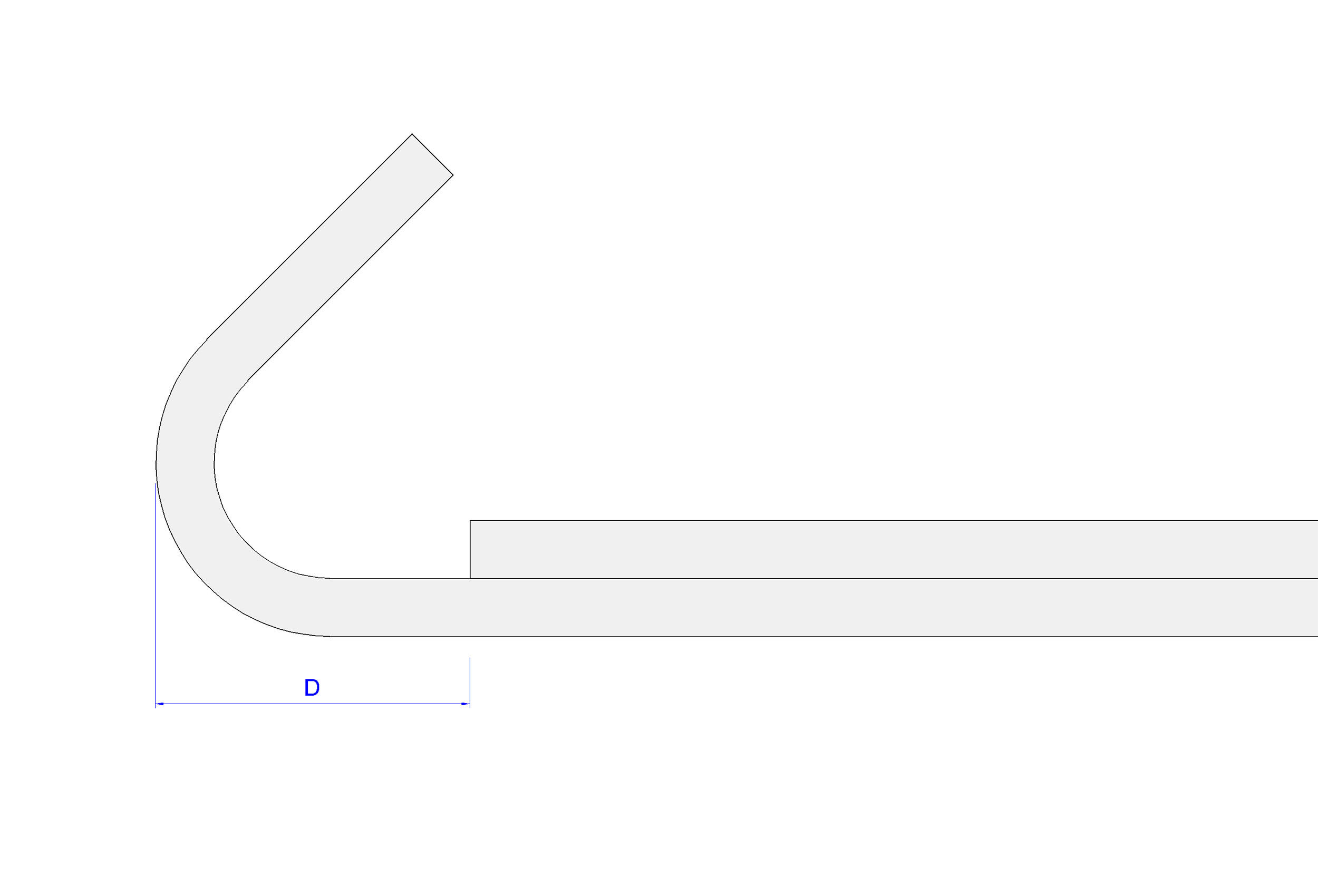
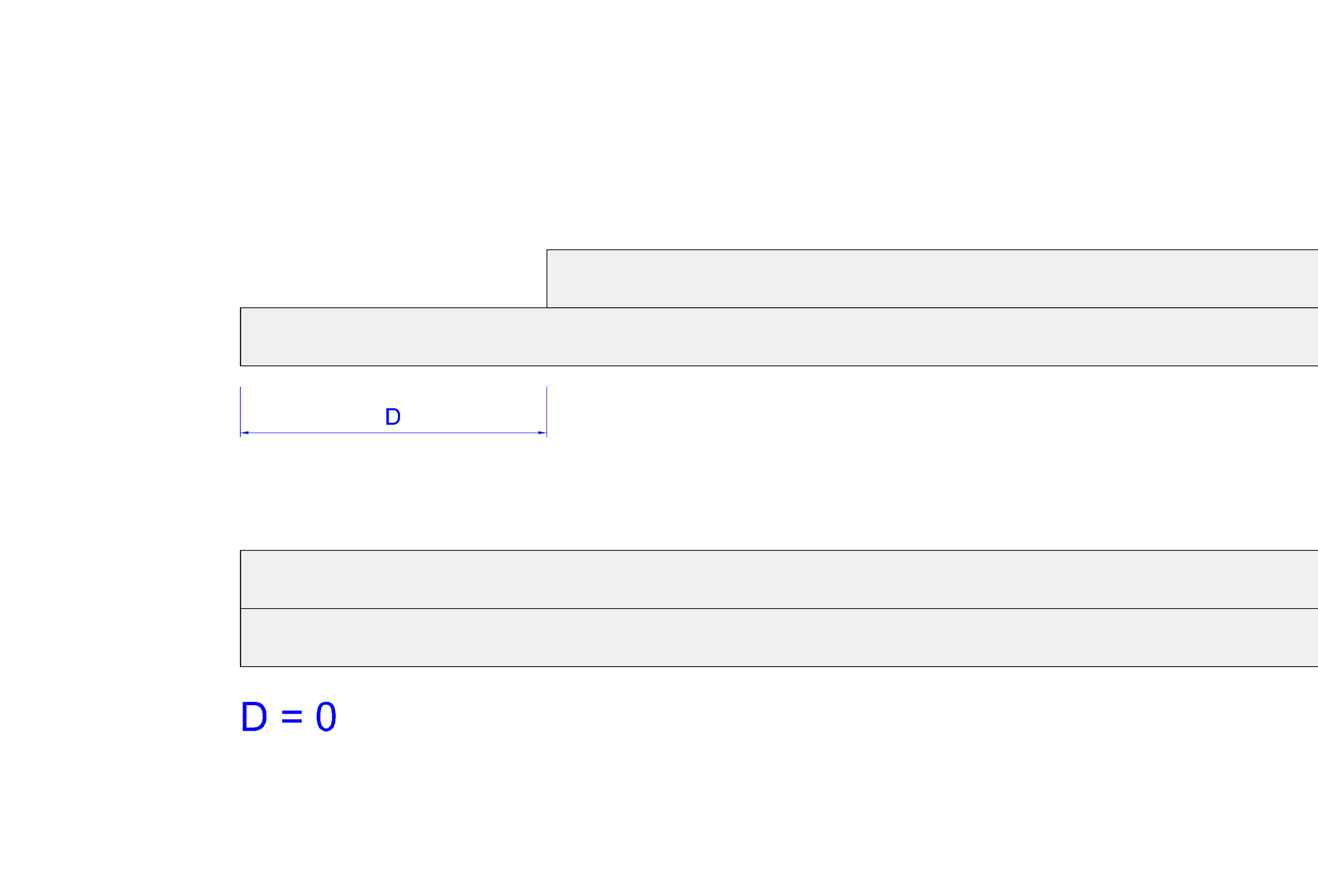
Dans le cadre du ferraillage de poutre, les valeurs D servent à indiquer le départ de chaque barre par rapport aux barres situées dans le lit 1 (inférieur). Ces départs sont déterminés en fonction de la position relative et de la forme de façonnage des barres précédentes, notamment celles du lit inférieur.
Pour garantir une application correcte des valeurs D, veuillez consulter l'image ci-dessous.
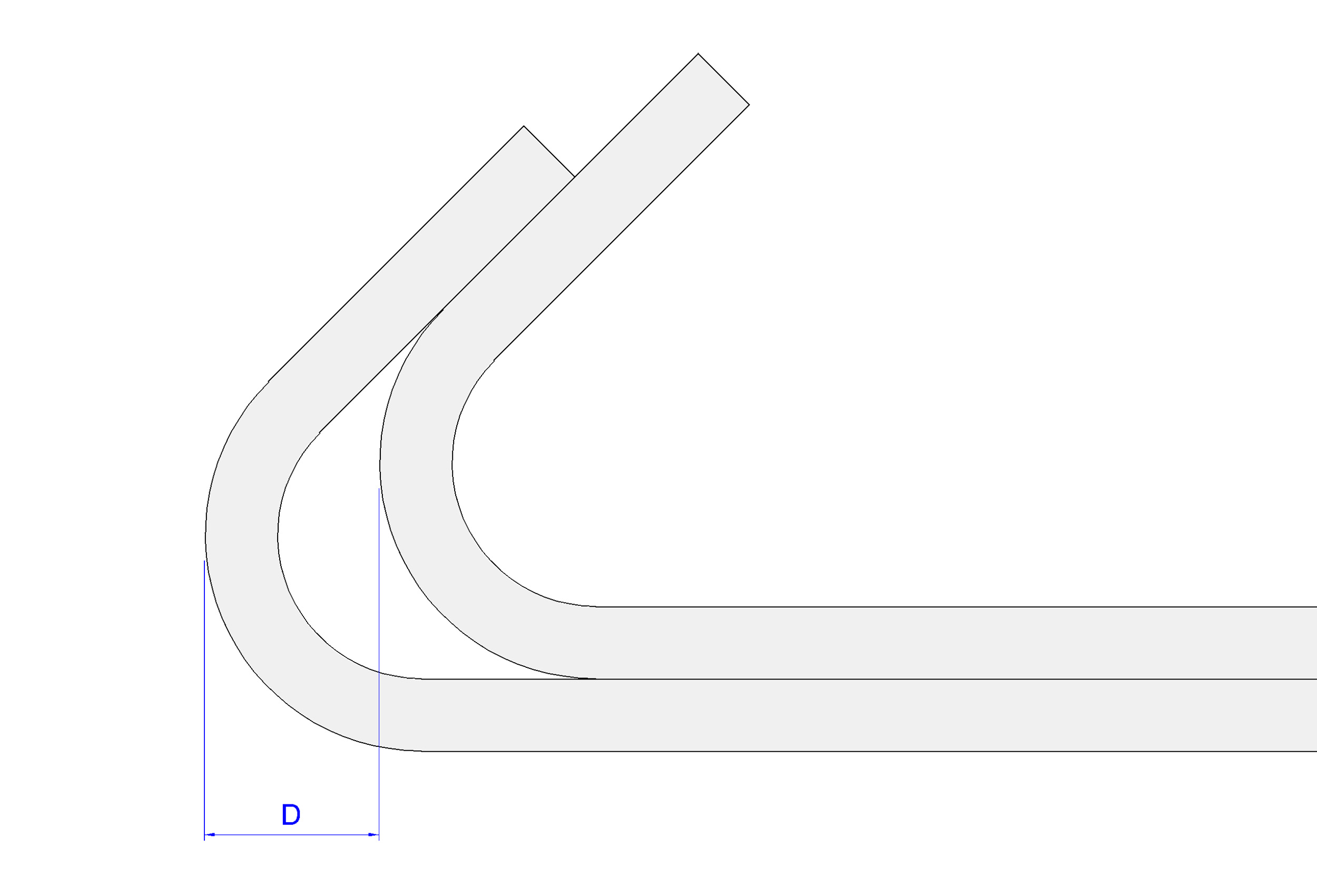
Les tableaux de calcul, la nomenclature et les schémas de disposition présentés ci-dessus offrent une base solide pour le dimensionnement des poutres isostatiques en béton armé, dans le respect des prescriptions de l’Eurocode 2. Ils constituent un support pédagogique et pratique pour l’apprentissage comme pour la conception.
Tous les résultats doivent impérativement être validés par un bureau d’études qualifié avant toute mise en œuvre sur chantier. Bien que l’outil applique les règles de calcul de l’EC2, l’utilisateur reste responsable de l’interprétation et de l’utilisation des données. L’objectif est de fournir une aide transparente et reproductible, mais non de remplacer l’expertise professionnelle.
L’outil est distribué en logiciel libre et open source, afin de garantir son auditabilité, son amélioration collaborative et sa réutilisation dans d’autres environnements numériques. Cette approche favorise l’interopérabilité et contribue au bien commun en rendant accessibles à tous des méthodes de calcul normalisées.
La fonction d’export au format PDF sera prochainement disponible, afin de faciliter l’archivage et le partage des résultats dans des processus de conception intégrés (par ex. workflows BIM).
Pour signaler toute erreur, suggestion ou dysfonctionnement, merci d’utiliser la page Contactez-nous ou de contribuer directement via le dépôt GitHub. Vos retours sont essentiels pour améliorer en continu cet outil au service de la communauté.
Merci de votre confiance — nous espérons que ce calculateur libre vous accompagnera efficacement dans vos projets de conception et de dimensionnement.