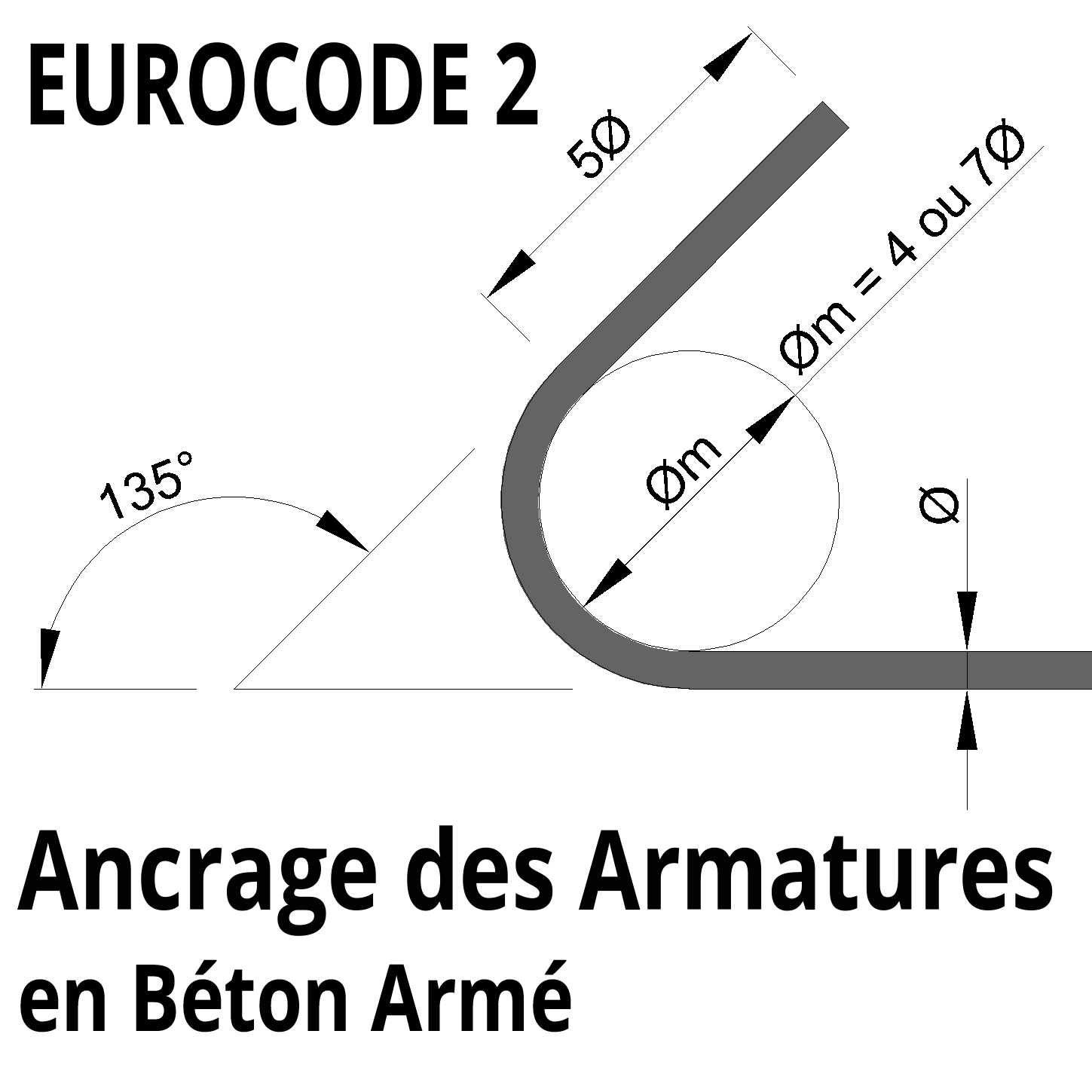
L’ancrage est un terme utilisé dans le domaine du béton armé pour décrire le processus par lequel les barres d’acier, également appelées armatures, sont fixées au béton lors de la procédure de ferraillage, garantissant ainsi une bonne adhérence entre les deux matériaux.
L’objectif principal de l’ancrage est de prévenir le mouvement ou l’extrusion de l’armature hors de la structure en béton sous l’effet de diverses charges, comme le poids de la structure elle-même, les charges externes ou encore les forces dynamiques.
Sur cette page, vous découvrirez tous les aspects essentiels de l’ancrage : les différents types, les méthodes détaillées de calcul, et la détermination des longueurs et formes d’ancrage conformément à la norme Eurocode 2.
L'ancrage consiste à fixer une barre d'acier à son extrémité au béton, afin qu'ils puissent fonctionner ensemble de manière efficace.
Pour résister à un effort spécifique, une barre d'acier doit posséder une résistance adéquate et être correctement ancrée pour absorber l'effort.
La forme la plus courante d'ancrage est l'ancrage droit, qui est simple et efficace.
Cependant, dans les situations où l'espace est limité et ne permet pas le développement complet d'un ancrage droit, un ancrage courbe peut être utilisé. Cette méthode est particulièrement utile aux extrémités des poutres. De plus, l'ancrage courbe est souvent utilisé comme mesure de sécurité lorsqu'il y a des doutes sur la qualité de l'adhérence entre la barre et le béton.
L'ancrage droit est la méthode la plus courante et simple pour fixer les armatures en acier dans le béton armé. Il consiste à insérer directement une barre d'acier dans le béton sans courber ou modifier son extrémité.
Avec cette méthode, la solidité des ancrages droits dépend uniquement de l’adhérence entre le béton et l’armature.
L’ancrage droit est largement utilisé et adapté à de nombreuses applications structurelles, notamment les dalles, les fondations et les poteaux, en raison de sa simplicité et de son efficacité.
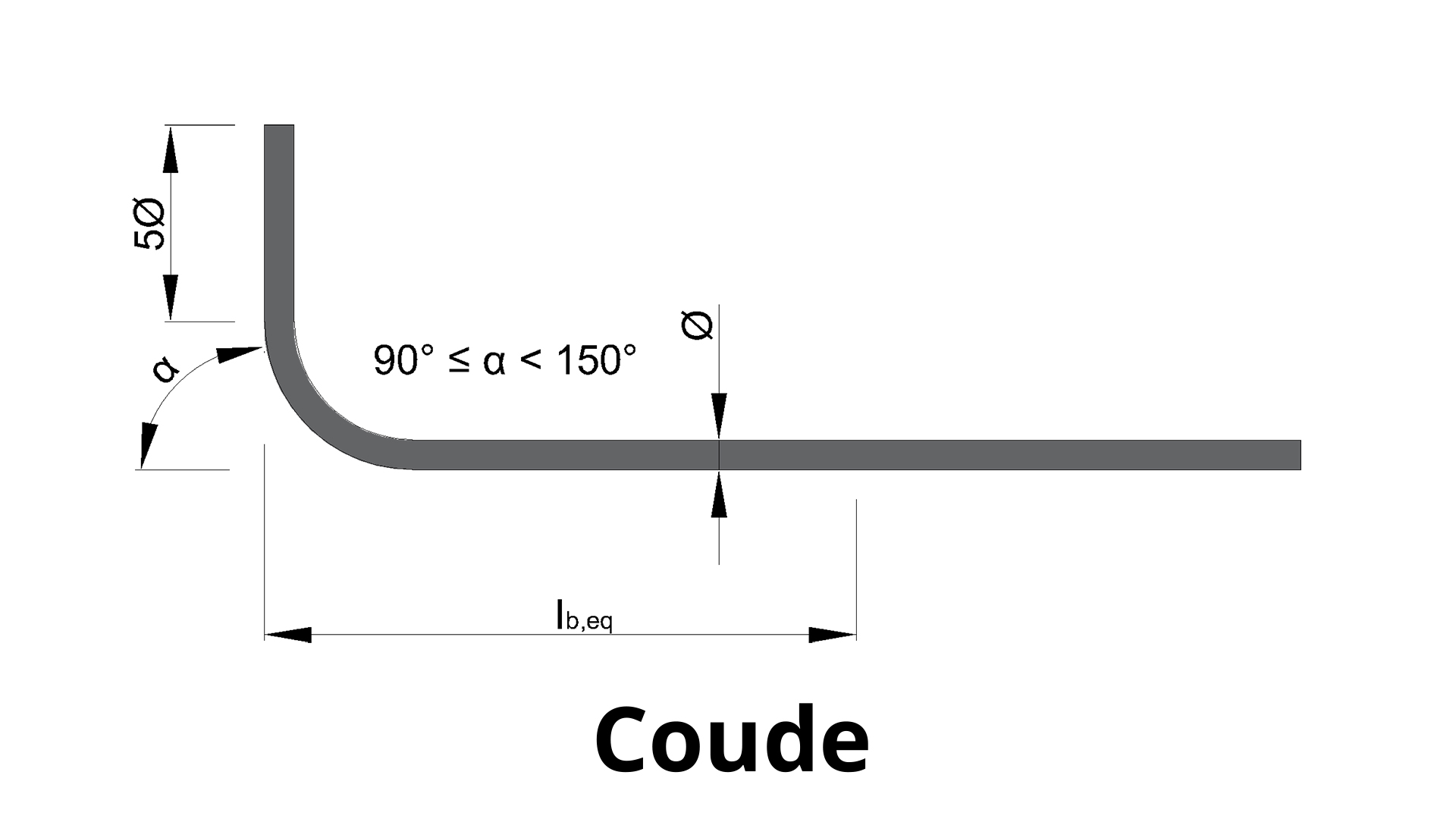
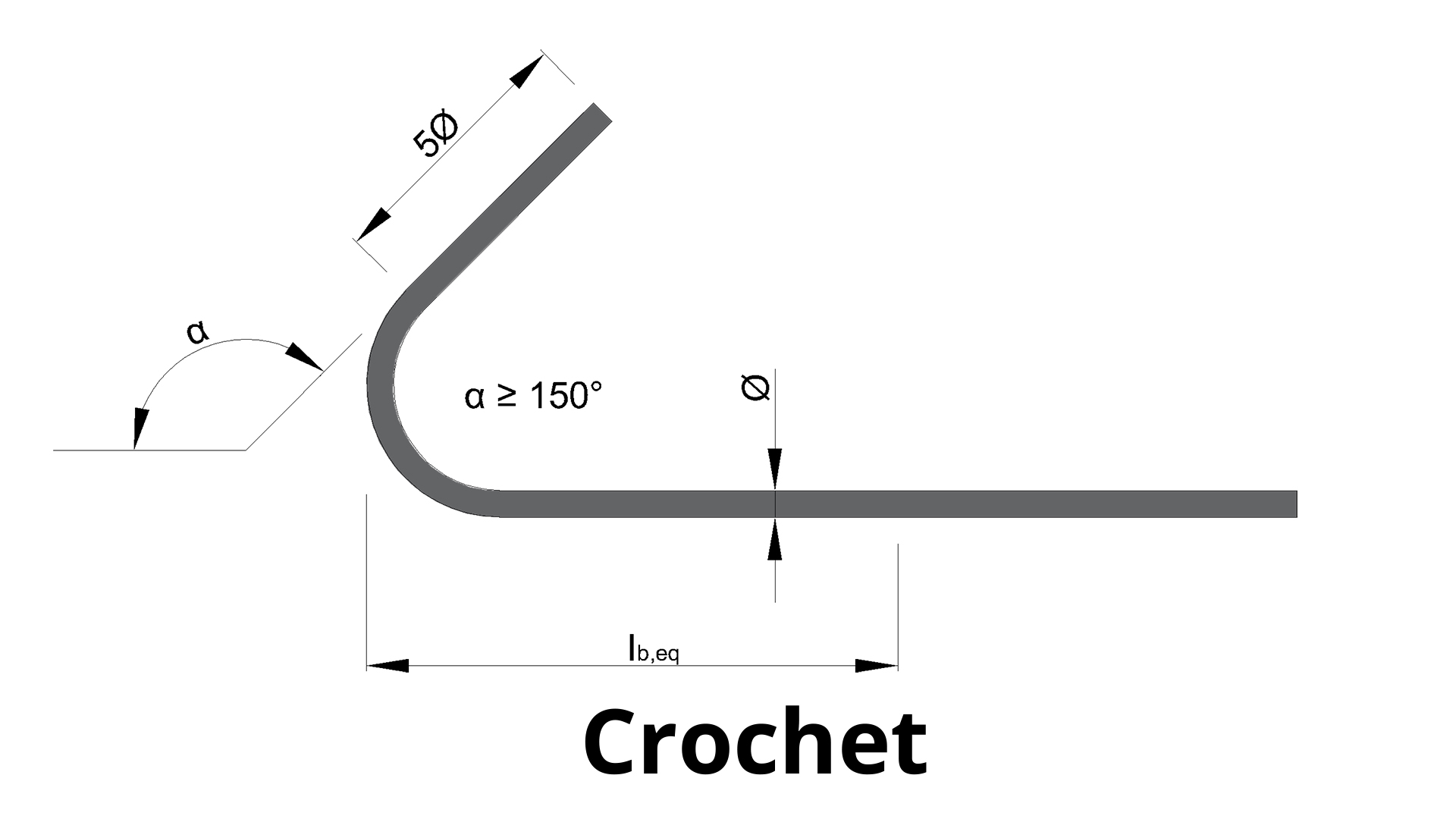
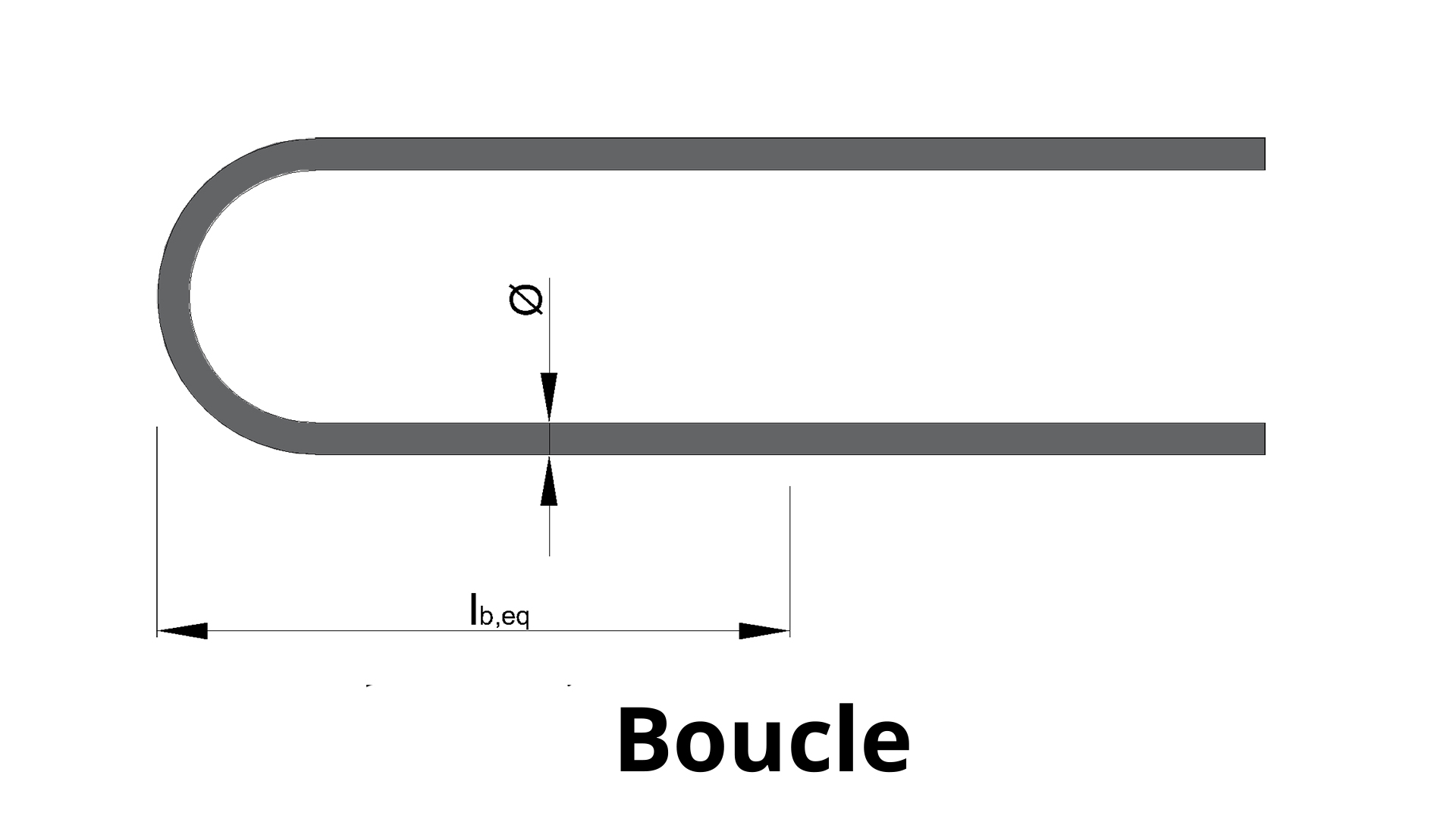
Les ancrages courbes, également connus sous le nom de crochets, sont caractérisés par des retours d'armature formant un angle compris entre 90° et 180°. Leur conception et leur utilisation sont régies par l'Eurocode 2, qui établit des normes précises pour garantir la sécurité et l'efficacité des structures.
L’Eurocode définit la géométrie des trois types principaux d’ancrages courbes :
Ces ancrages courbes présentent plusieurs caractéristiques importantes à prendre en compte :
Restriction en compression :
L'utilisation des ancrages courbes n'est pas autorisée pour les armatures en compression. Cette limitation vise à éviter les risques potentiels liés au comportement de ces ancrages sous des efforts de compression.
Efficacité théorique :
Contrairement à ce que l'on pourrait penser, l'Eurocode 2 n'attribue pas aux ancrages courbes une efficacité théorique supérieure à celle des ancrages droits. Cela signifie que, du point de vue normatif, ils ne sont pas considérés comme intrinsèquement plus performants que leurs homologues droits.
Fonctionnement :
Un ancrage courbe agit essentiellement comme un ancrage droit replié sur lui-même. Cette configuration offre certains avantages en termes d'espace, nécessitant moins de longueur parallèle à l'axe de la barre par rapport à un ancrage droit classique. Cependant, cela se fait au prix d'un besoin accru d'espace perpendiculaire à cet axe.
Effet d'obstacle :
Au-delà de son fonctionnement de base, l'ancrage courbe bénéficie d'un effet d'obstacle supplémentaire. La partie courbée du crochet s'appuie directement sur le béton environnant, créant ainsi une résistance additionnelle.
Lorsque le béton résiste efficacement, l’ancrage ne peut céder que par glissement et déroulement du crochet, ce qui provoque une rupture ductile de l’ancrage.
Pression sur le béton :
L'effet d'obstacle généré par le crochet induit une pression sur le béton situé à l'intérieur de la courbure. Si le crochet s’étend parallèlement et près d’une surface, cette pression peut causer la rupture du béton et neutraliser l’ancrage. Il est important de noter que l'intensité de cette pression est inversement proportionnelle au rayon de courbure du crochet : plus le rayon est petit, plus la pression exercée sur le béton est élevée.
Précautions pour les crochets à 90° :
Les crochets formant un angle droit (90°) nécessitent une attention particulière lors de leur mise en œuvre. Si le retour de ces crochets est orienté parallèlement à une surface du béton, le processus de déroulement du crochet sous tension peut créer un effet de "poussée au vide". Ce phénomène augmente considérablement le risque d'éclatement du béton d'enrobage. Pour prévenir ce problème, le segment qui se déroule en poussant vers le vide doit être maintenu par un acier ancré dans le volume du béton.
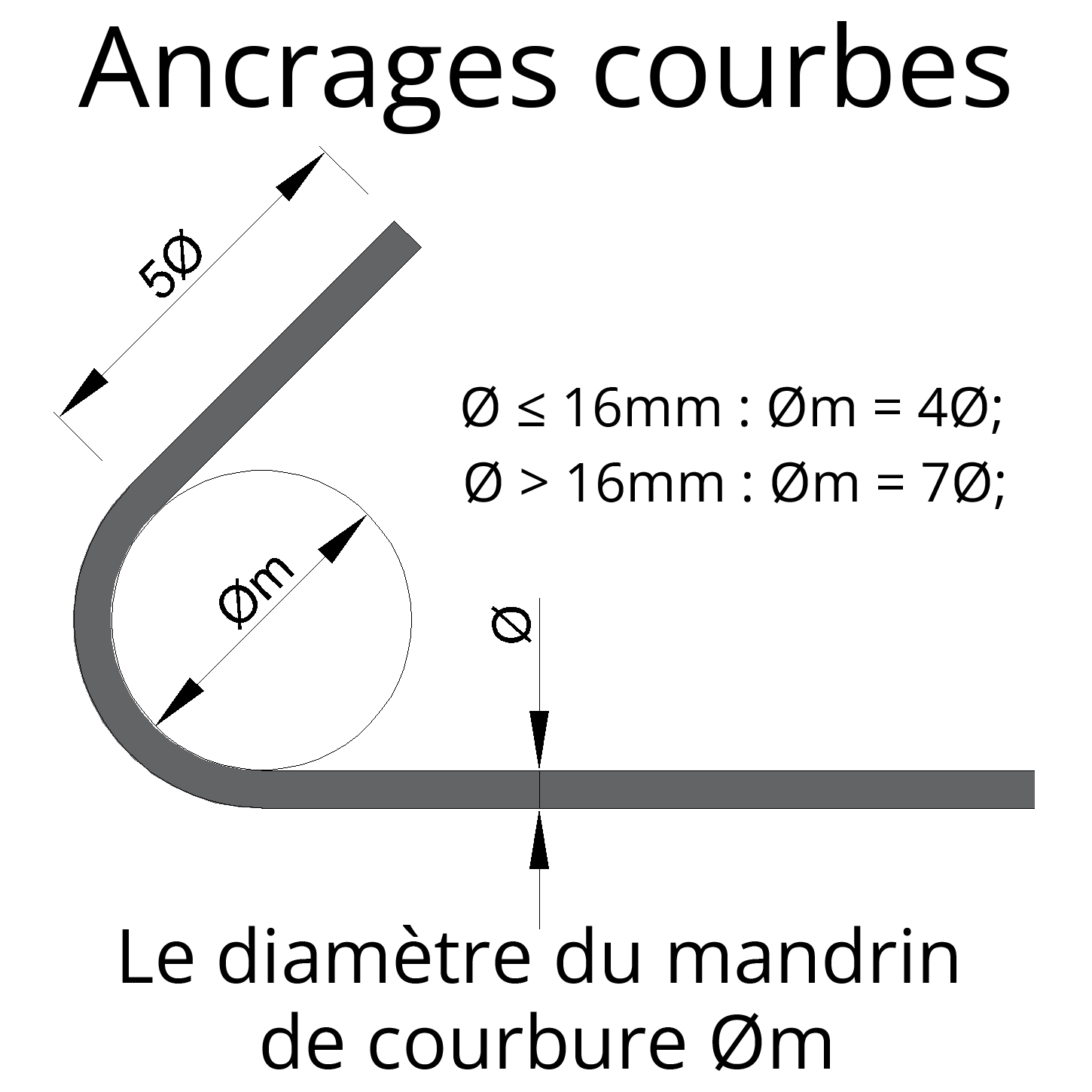
L'Eurocode 2 définit les diamètres minimaux des mandrins utilisés pour les coudes, crochets ou boucles des armatures en fonction du diamètre de la barre.
Pour les barres d'armature de diamètre inférieur ou égal à 16 mm, le diamètre minimal du mandrin doit être de 4 fois le diamètre de la barre :
∅min = 4*∅.
Pour les barres de diamètre supérieur à 16 mm, le diamètre minimal du mandrin doit être de 7 fois le diamètre de la barre :
∅min = 7*∅.
Lorsque des soudures sont présentes dans la partie courbe de l'ancrage, le diamètre minimal du mandrin est légèrement augmenté pour garantir une meilleure performance structurelle. Dans ce cas, le diamètre du mandrin doit être de 5 fois le diamètre de la barre :
∅min = 5*∅.
Lorsqu’un effort est exercé sur un ancrage courbe, il comprime le béton à l’intérieur de la courbure. Pour prévenir la fissuration du béton, les armatures doivent présenter une courbure minimale et être suffisamment enrobées de béton. Selon l’Eurocode, il n’y a pas de risque de fissuration du béton si l’une des deux conditions suivantes est respectée :
Dans les constructions courantes, la deuxième condition est généralement respectée dans les trois cas suivants :
Si ces deux conditions ne sont pas respectées, il y a un risque de fissuration du béton. Dans ce cas, pour éviter la fissuration du béton, il est indispensable de vérifier les conditions de non-écrasement du béton à l’intérieur de la courbure. Si ces conditions ne sont pas respectées, il faut augmenter le diamètre de la courbure.
La courbure doit présenter un diamètre minimal de centrage (∅m) supérieur aux valeurs indiquées :
∅m ≥ Fbt * (1/ab + 1/(2*∅)) / fcd, où :
fcd : Résistance de calcul du béton en compression.
a : Distance entre les barres ou entre une barre et la face de la section (généralement entre les barres d'acier).
cd : Enrobage effectif utilisé pour le calcul, déterminé à partir de cmin, conformément aux règles de l'Eurocode 2.
ab : Distance entre axes des barres perpendiculaires au plan des courbures.
ab = cd + ∅/2.
Fbt : Effort dans la barre au point d’origine de la courbure.
Fbt = π*(∅²/4)*(1/fyd).
fyd : Résistance d'acier de calcul, où :
fyd = fyk/ɣs, avec fyk = 500 Mpa pour aciers B500B et ɣs = 1.15.
En cas d’ancrages des cadres, étriers ou épingles pour aciers transversaux, l’ancrage doit être correctement enroulé autour d’une barre des aciers principaux pour assurer une stabilité optimale.
Il existe deux types d’ancrages recommandés :
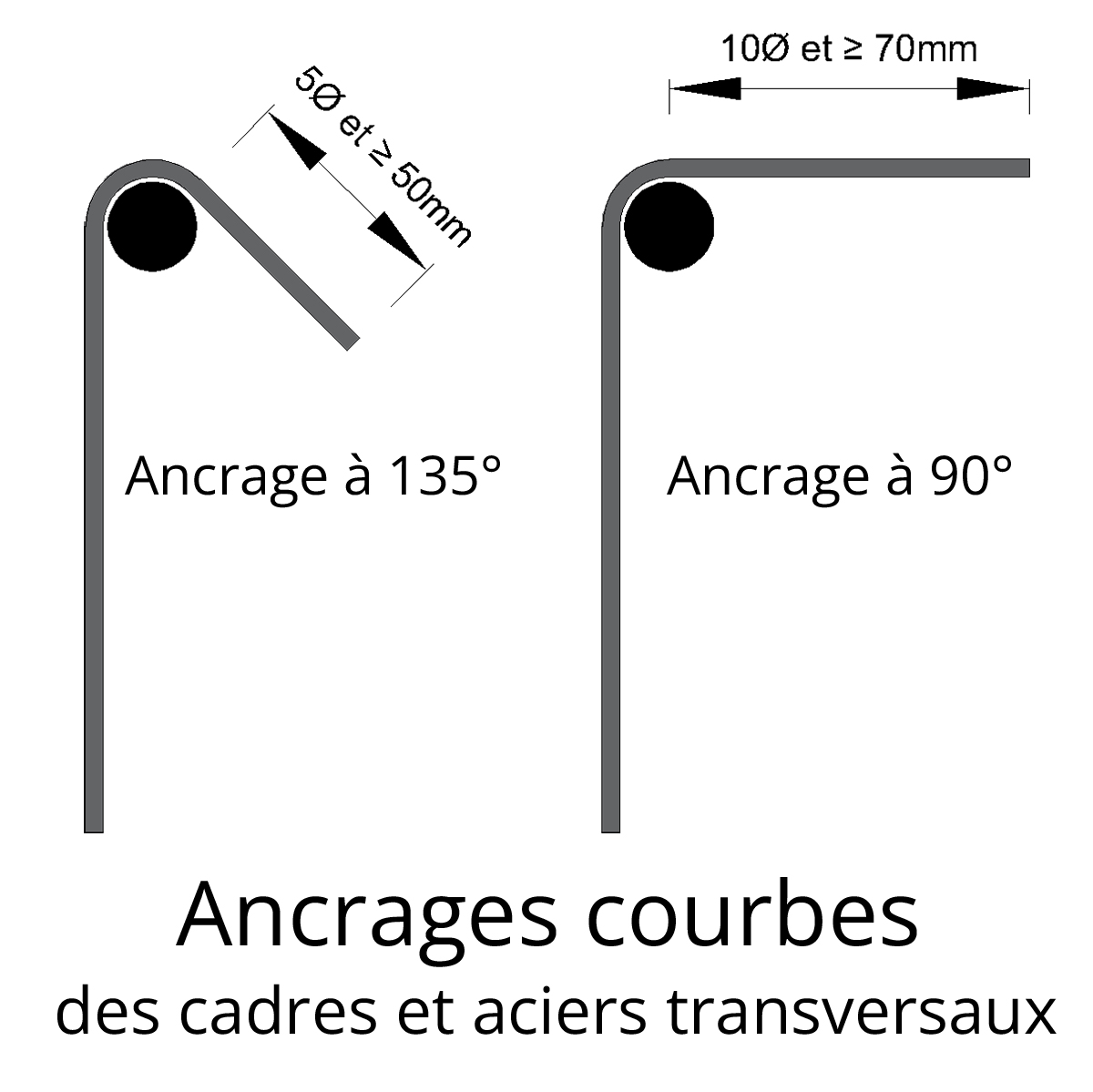
Le retour de l’ancrage doit être supérieur au maximum entre 5 fois le diamètre de la barre (5*∅) et 50 mm. En formule, cela donne :
Retour > max [5*∅ ; 50 mm].
Pour ce type, le retour de l’ancrage doit être supérieur au maximum entre 10 fois le diamètre de la barre (10*∅) et 70 mm. En formule :
Retour > max [10*∅ ; 70 mm].
L’Eurocode 2 fournit des directives précises pour déterminer la longueur d’ancrage lb en fonction du diamètre de la barre, de la limite d’élasticité des aciers (fyk), des caractéristiques du béton et des conditions d’adhérence.
La longueur d’ancrage de référence, désignée par lb,rqd, représente la longueur nécessaire pour un ancrage droit ou courbe avant l'application de coefficients correcteurs adaptés au contexte spécifique. Le terme lb,rqd utilise l’abréviation "rqd" pour "required" en anglais, signifiant "requis".
Pour déterminer cette longueur en supposant une contrainte d'adhérence constante égale à fbd, on utilise la formule suivante pour ancrer une barre de diamètre ∅ sous un effort Fsd = As * σsd :
lb,rqd = (∅/4) * (σsd/fbd),
ou
la contrainte σsd représente la contrainte de calcul de la barre dans la section à partir de laquelle on mesure l'ancrage :
σsd = fyd = fyk/ɣs.
Typiquement, pour des aciers de 500 MPa, cette contrainte est de 435 MPa dans les conditions maximales. Sinon, on peut calculer la valeur exacte en fonction du chargement spécifique.
Et, fbd désigne la valeur de calcul de la contrainte ultime d'adhérence entre le béton et l’armature.
La contrainte d'adhérence ultime entre le béton et l'armature, notée fbd, est déterminée par la formule suivante :
fbd = 2,25*η1*η2*fctd.
Facteurs de condition :
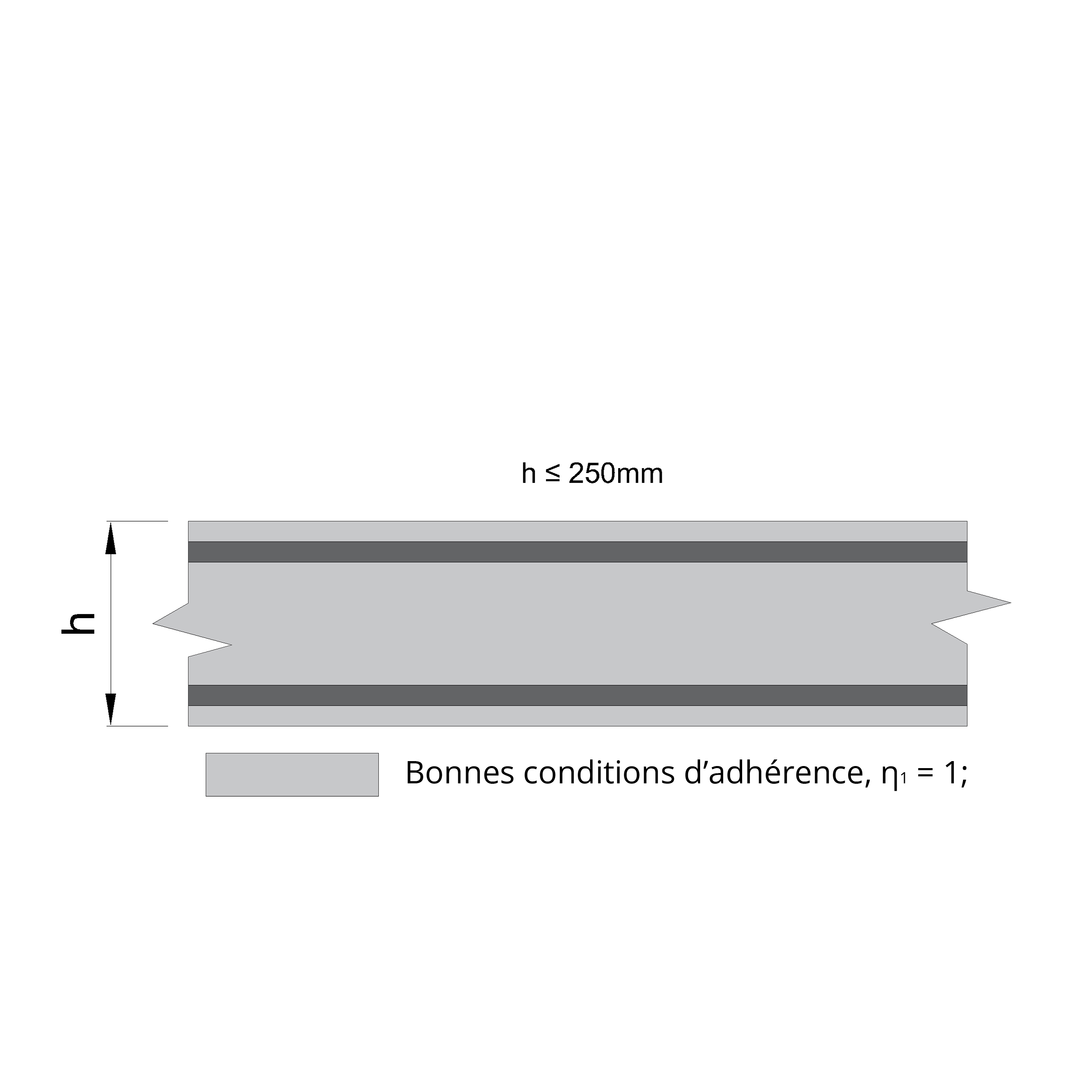
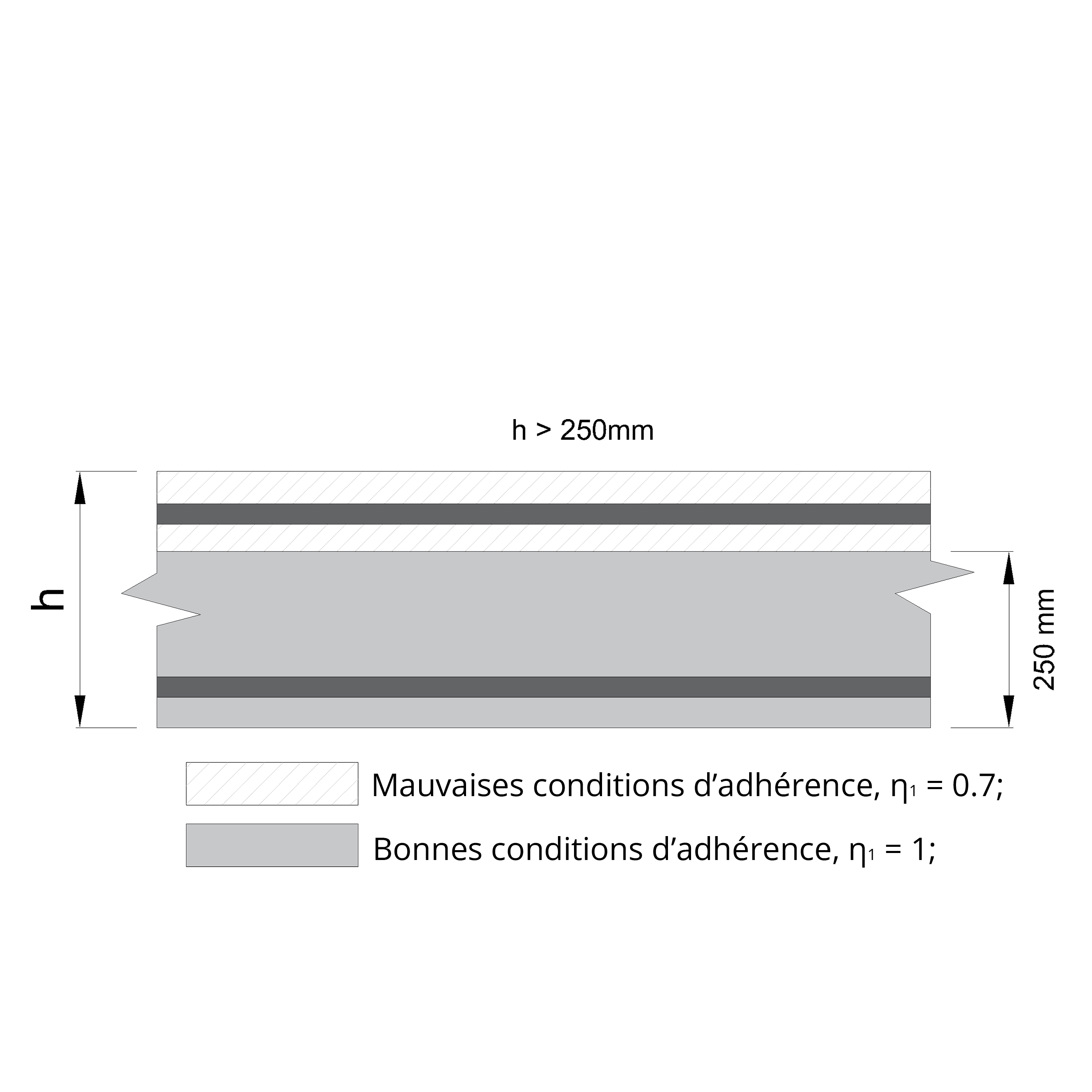
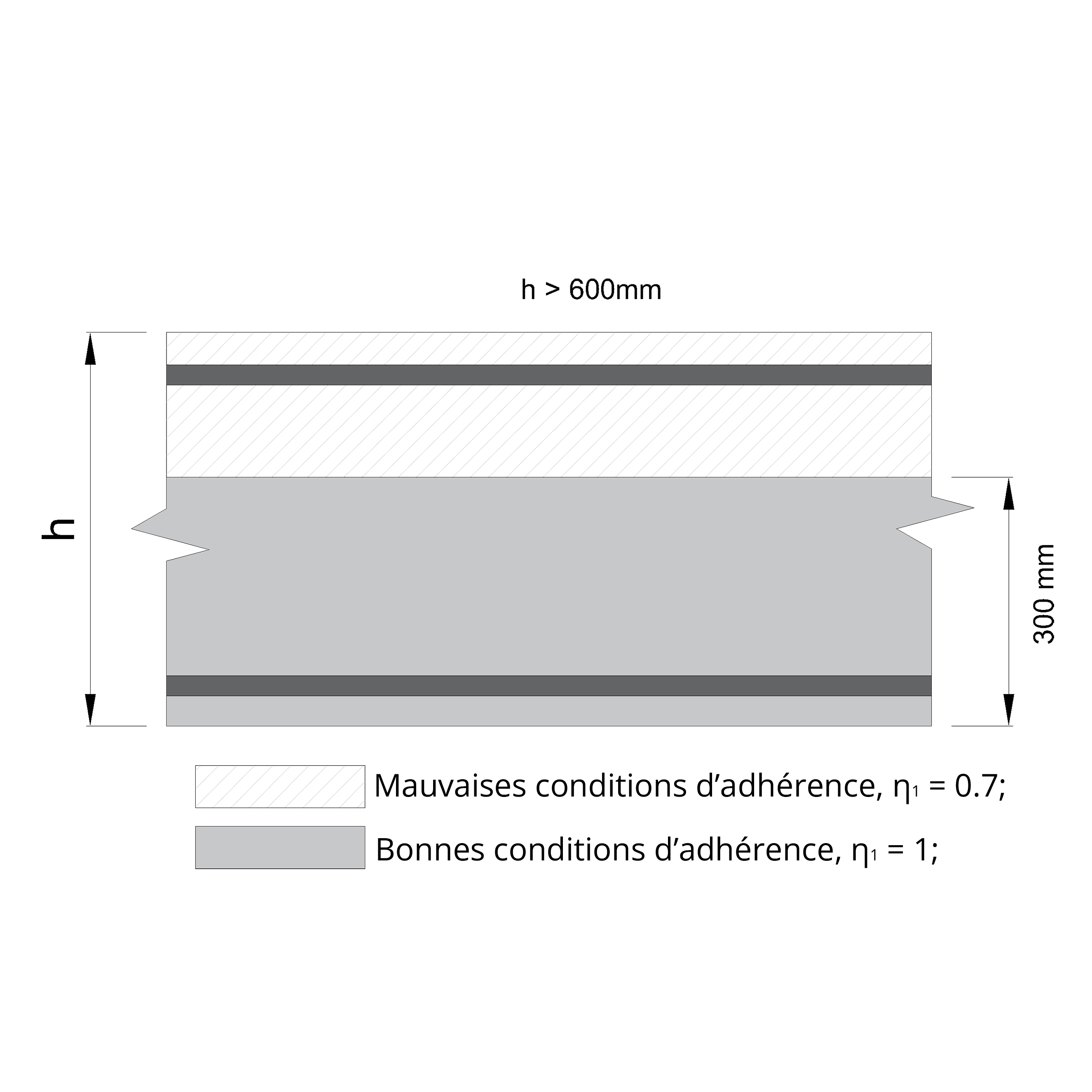
η1 représente les conditions d’adhérence:
η1 = 1 pour de bonnes conditions d’adhérence,
η1 = 0.7 pour de mauvaises conditions d’adhérence.
η2 dépend du diamètre de la barre d'armature ∅ :
η2 = 1 si ∅ ≤ 32 mm,
η2 = (132 – ∅)/100 si ∅ est supérieur à 32 mm.
Pour des bétons avec une résistance caractéristique à la compression fck inférieure à 60 MPa, la résistance à la traction de calcul du béton fctd est donnée par :
fctd = fctk,0.05 / γc = (0,21*fck 2/3)/γc, avec γc = 1,5.
| fck | 12 | 16 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 60 |
|---|---|---|---|---|---|---|---|---|---|---|
| fctk,0.05 | 1,1 | 1,3 | 1,5 | 1,8 | 2 | 2,2 | 2,5 | 2,7 | 2,9 | 3,1 |
| fctd | 0,7 | 0,8 | 1 | 1,2 | 1,3 | 1,5 | 1,7 | 1,8 | 1,9 | 2,1 |
| fbd | 1,7 | 2 | 2,3 | 2,7 | 3 | 3,4 | 3,75 | 4 | 4,3 | 4,6 |
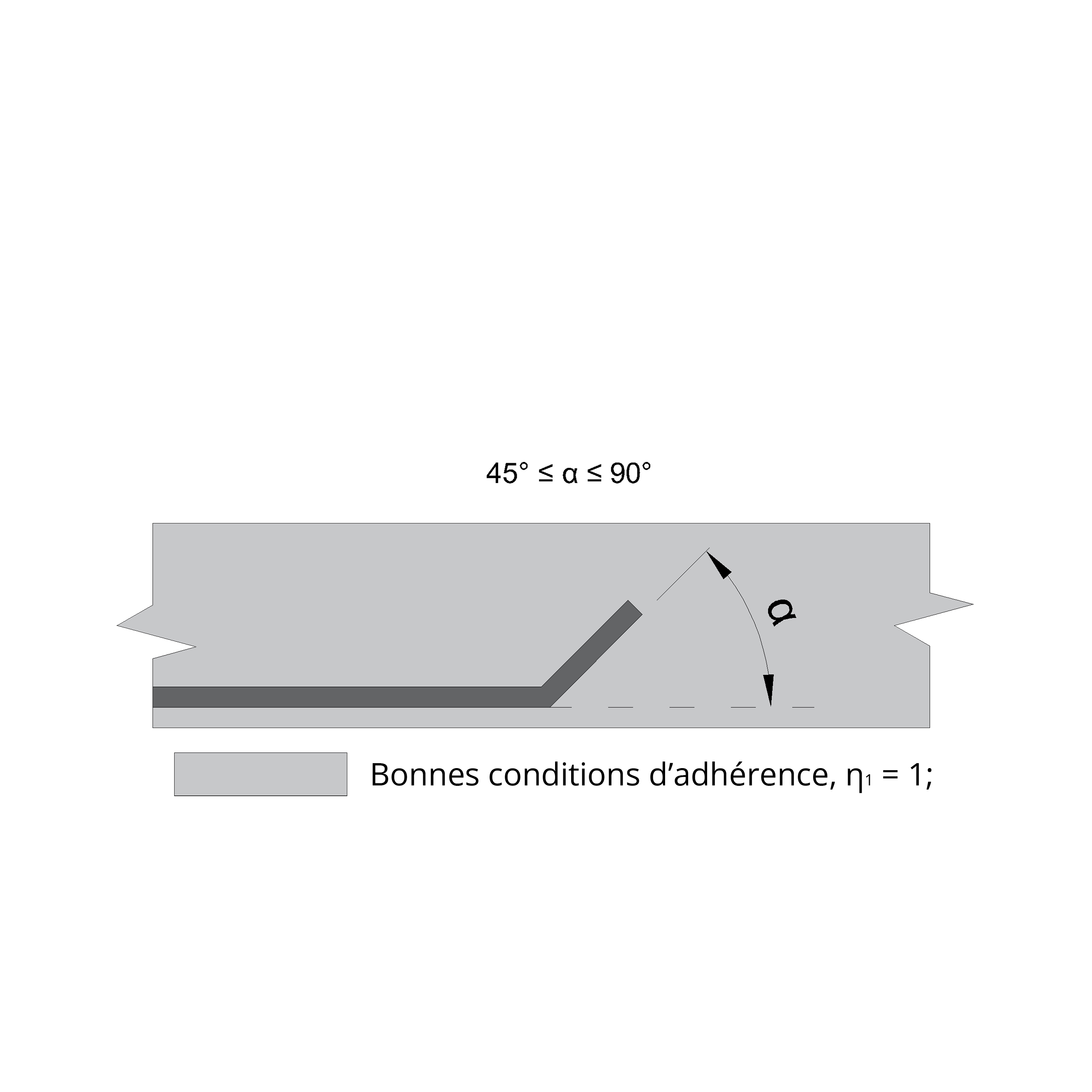
L'Eurocode 2 (EC2) définit les conditions nécessaires pour garantir une bonne adhérence entre le béton et l'acier d'armature. Pour assurer cette adhérence, les barres d'armature doivent respecter certaines inclinaisons et positions lors du bétonnage.
Inclinaison des barres :
Les barres doivent avoir une inclinaison comprise entre 45° et 90° par rapport à l'horizontale. Cette inclinaison permet un enrobage optimal du béton autour des barres, améliorant ainsi l'adhérence.
Inclinaison inférieure à 45° :
Si l'inclinaison des barres est inférieure à 45°, des mesures supplémentaires sont nécessaires. Les barres doivent être noyées dans un élément de béton d'une hauteur inférieure à 25 cm.
Si l'élément de béton est plus haut, les barres doivent être situées dans la moitié inférieure de l'élément ou à au moins 30 cm du haut de l'élément, selon la valeur la plus grande : min [h/2 ; 30 cm].
Ces conditions garantissent que les barres d'armature bénéficient d'un enrobage adéquat et d'une adhérence suffisante entre acier et béton.
(pour des aciers HA de limite fyk = 500 MPa)
| fck : | 12 | 16 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 60 |
|---|---|---|---|---|---|---|---|---|---|---|
| fbd (η1 = 1) bonne adhérence: | 1,7 | 2 | 2,3 | 2,7 | 3 | 3,4 | 3,7 | 4 | 4,3 | 4,6 |
| lb,rqd/∅ : | 64 | 54 | 47 | 40 | 36 | 32 | 29 | 27 | 25 | 24 |
| fbd (η1 = 0,7) mauvaise adhérence: | 1,2 | 1,4 | 1,6 | 1,9 | 2,1 | 2,4 | 2,6 | 2,8 | 3 | 3,2 |
| lb,rqd/∅ : | 91 | 78 | 68 | 57 | 52 | 45 | 42 | 39 | 36 | 34 |
La longueur d’ancrage de calcul, notée lbd, représente la longueur d’ancrage de référence lb,rqd, ajustée par une série de coefficients αi pour prendre en compte des spécificités qui nécessitent une adaptation par rapport au cas standard.
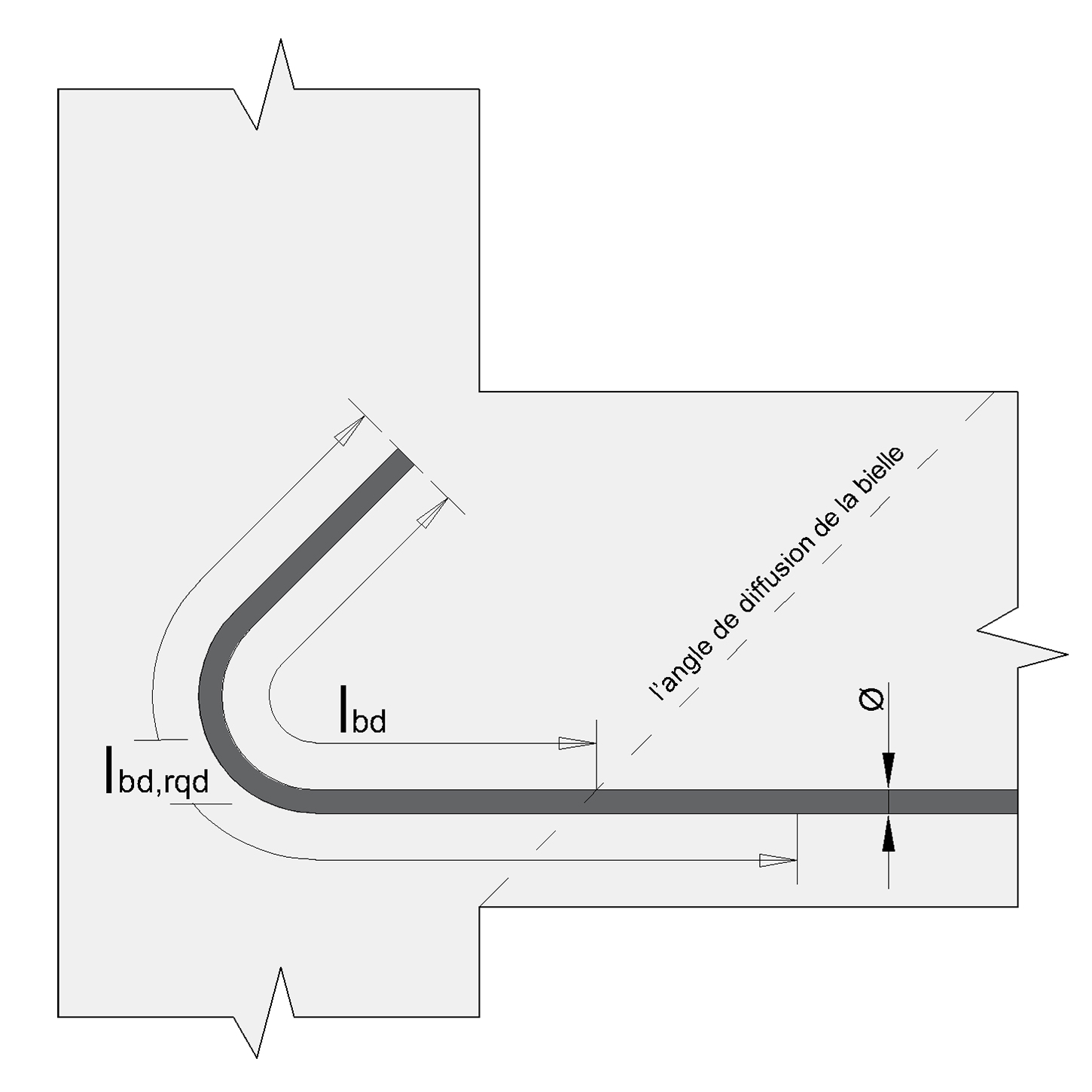
La longueur d’ancrage des armatures d’une poutre est déterminée à partir du point d’appui nu, en tenant compte de l’angle de diffusion de la bielle.
Pour les barres pliées, la longueur d’ancrage calculée lbd est déterminée en suivant la trajectoire développée de la barre.
La formule pour calculer lbd est la suivante :
lbd = α1*α2*α3*α4*α5*lb,rqd;
Les coefficients αi permettent d’ajuster la longueur d’ancrage de référence dans certaines circonstances.
En fonction des différentes conditions en traction (les barres d’armature sont soumises à des forces de tension), les coefficients αi sont définis comme suit :
𝛼1 : Ce coefficient ajuste la longueur en fonction de la forme de la barre, avec une réduction pour les barres courbes dans certaines conditions :
Barre droite : 𝛼1 = 1;
Barre courbe : α1 = 0,7 si cd > 3*∅.
𝛼2 : Ce coefficient tient compte de l’enrobage du béton autour de la barre, influençant la longueur d’ancrage requise :
Barre droite : 0,7 ≤ α2 = 1 – 0,15*( cd – ∅ ) / ∅ ≤ 1;
Barre courbe : 0,7 ≤ α2 = 1 – 0,15*( cd – 3*∅ ) / ∅ ≤ 1.
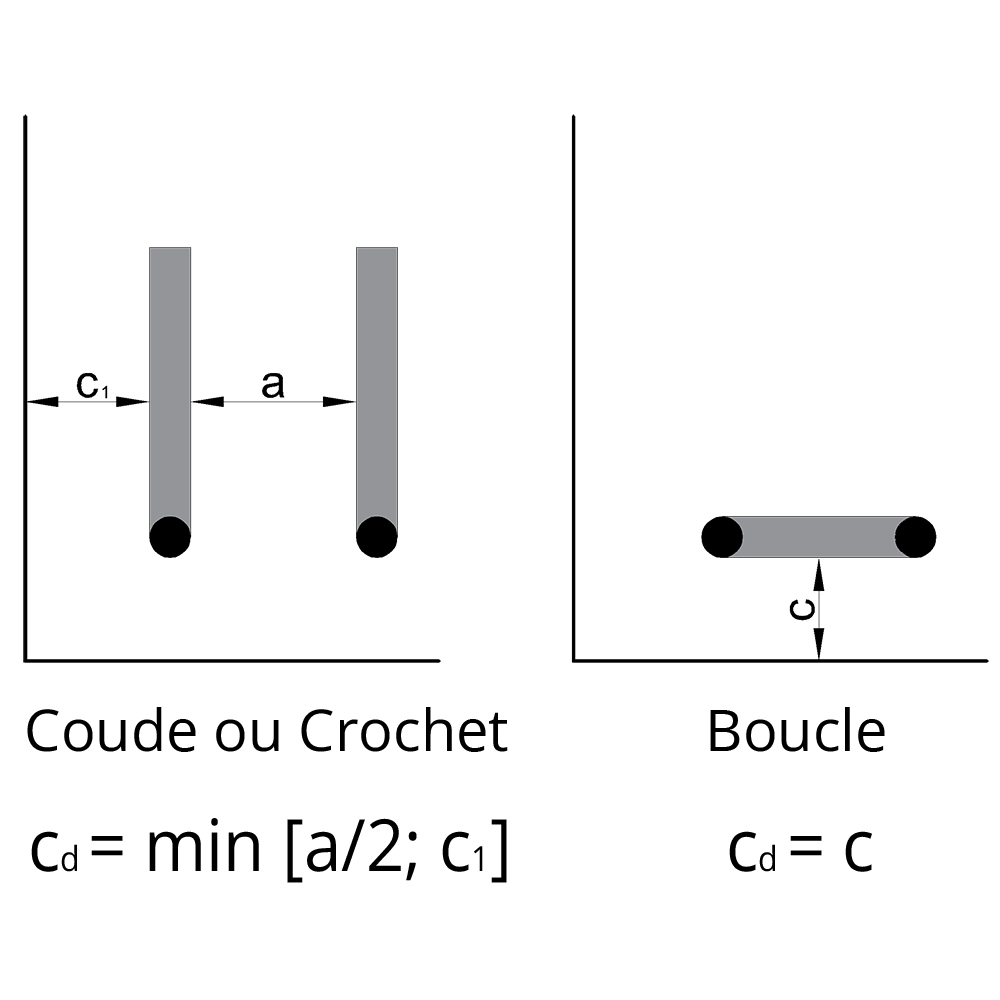
𝛼3 : Ce coefficient reflète l’effet des armatures transversales non soudées, qui peuvent améliorer le confinement de la barre :
Tout type d’ancrage : α3 = 1 – K*λ et 0,7 ≤ α3 ≤ 1.
Valeurs de k et λ :
λ = ( ∑ Ast – ∑ Ast,min ) / As ,
∑ Ast : section totale des armatures transversales non soudées le long de lbd.
∑ Ast,min : section minimale d'armatures transversales = 0.25As pour les poutres et 0 pour les dalles.
As : section de la barre ancrée.
k : vour les images ci-dessous:
L’indice ‘t’ fait référence à tout type d’acier transversal, il s’agit d’un acier qui est positionné perpendiculairement (à un angle de 90 degrés) par rapport à la barre ou à l’armature en question.
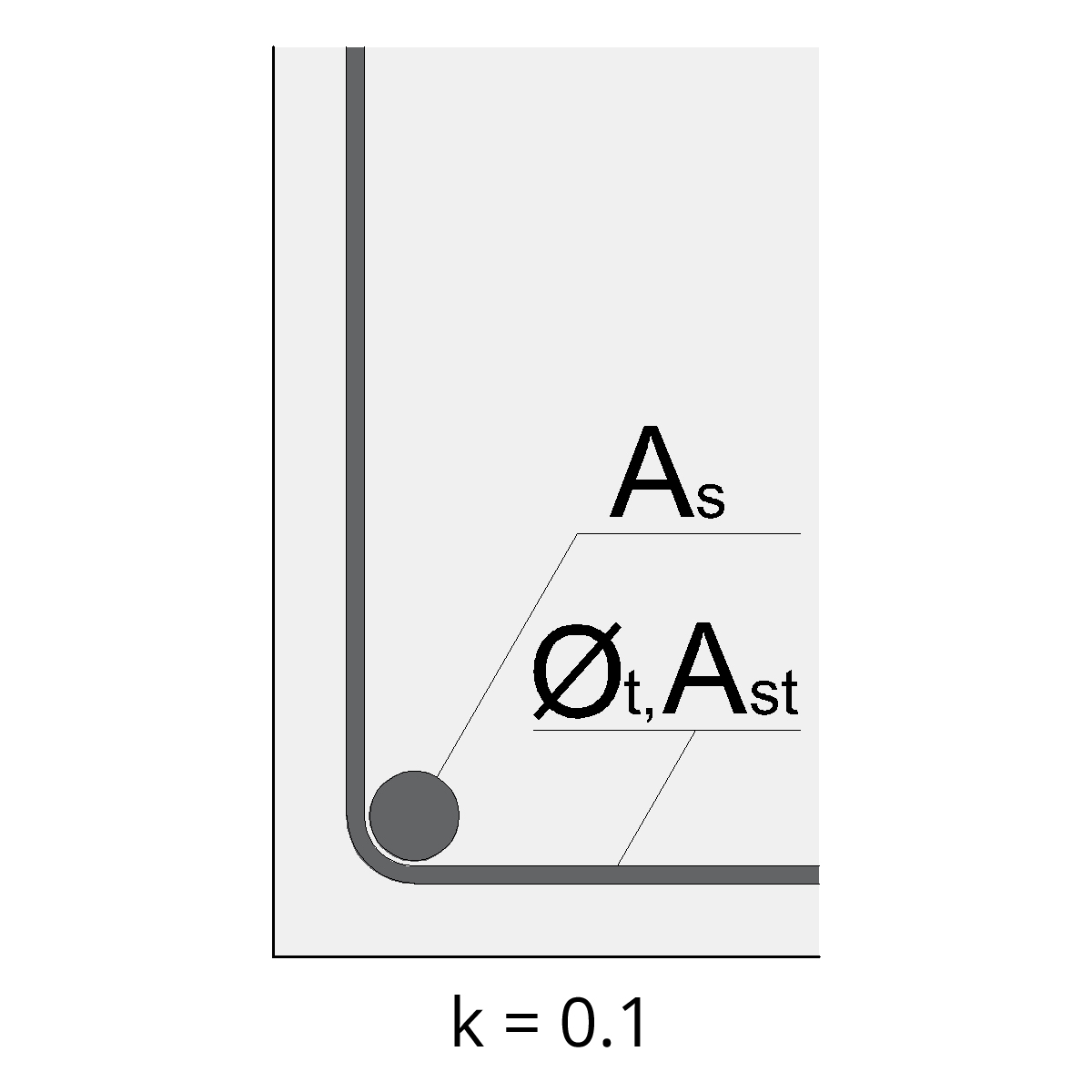
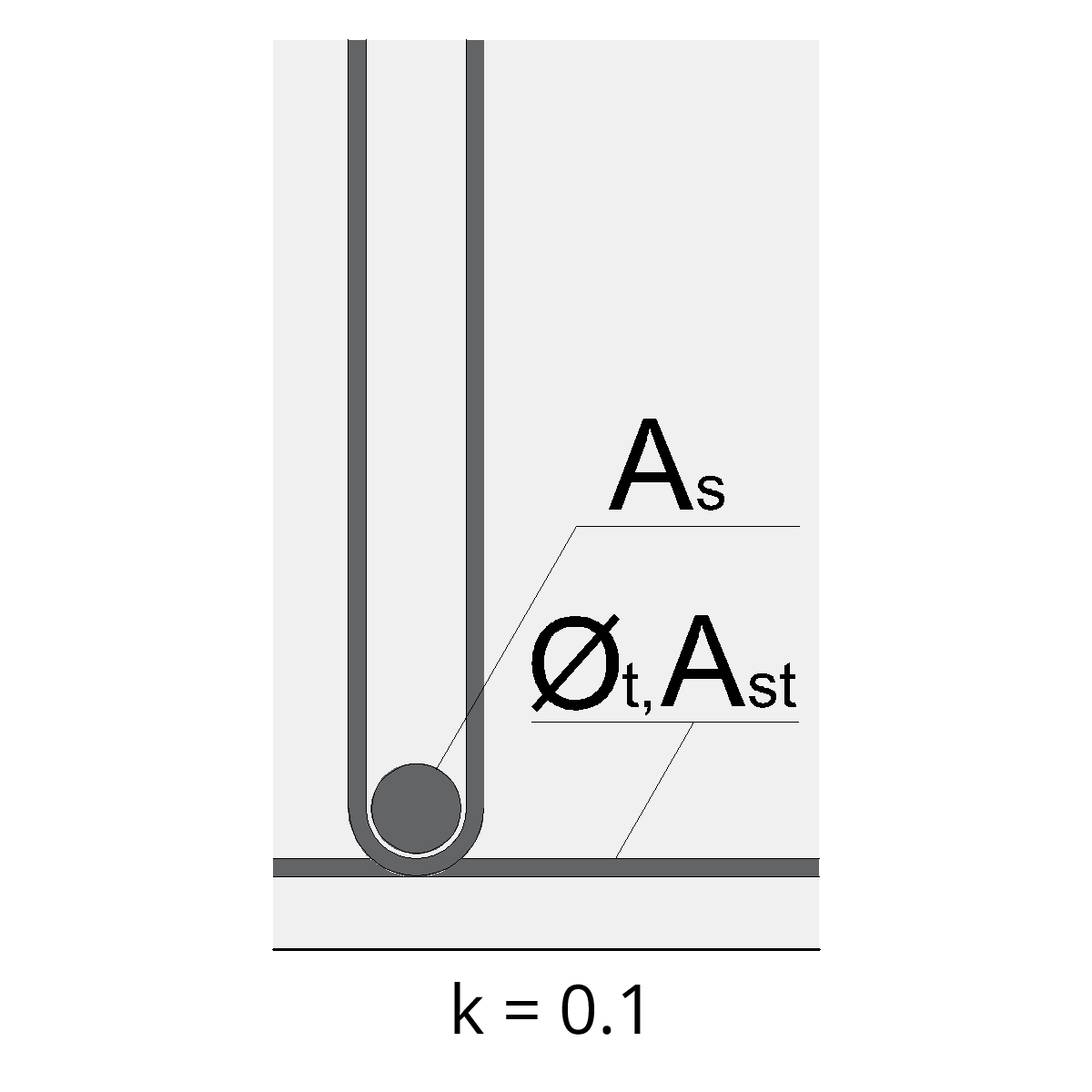
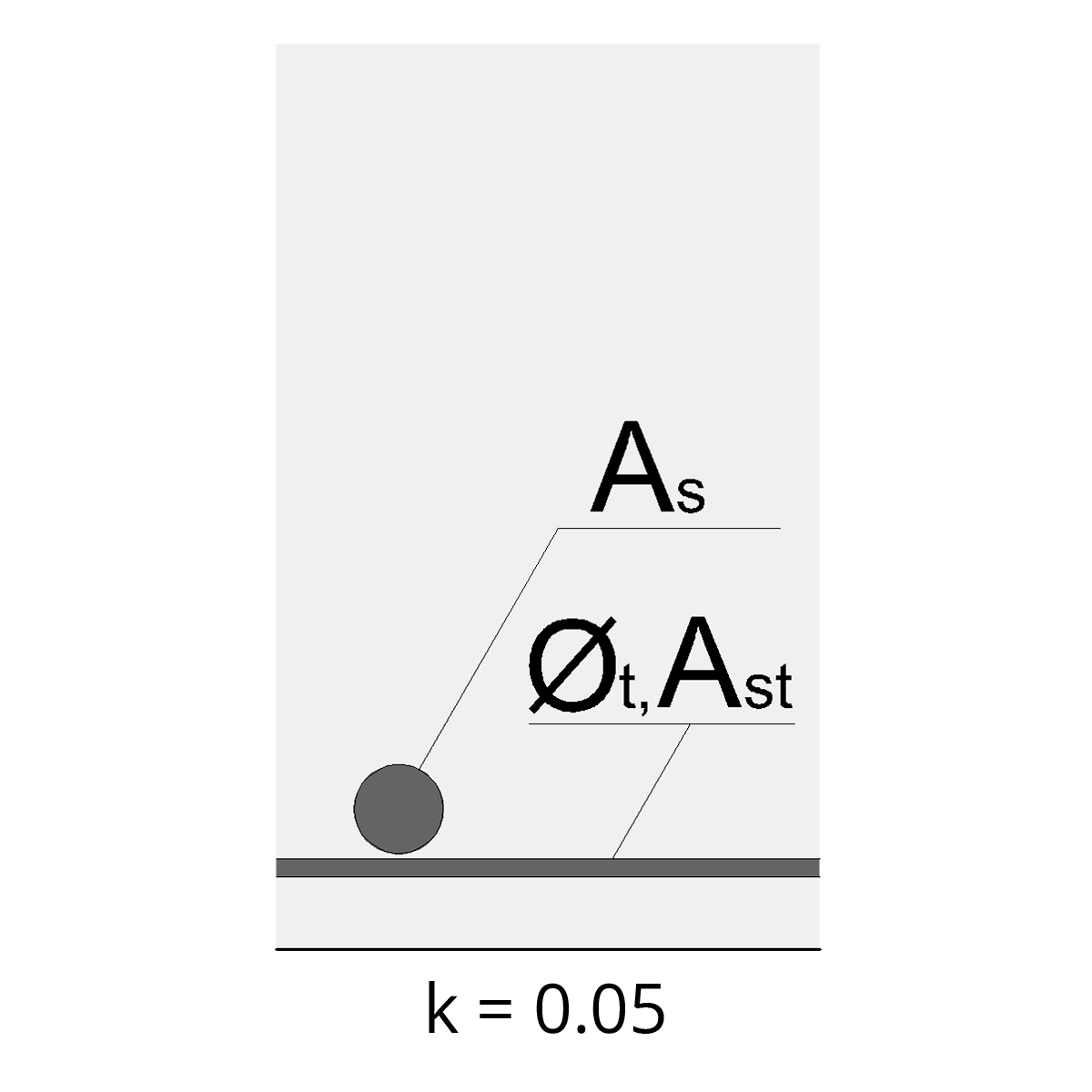
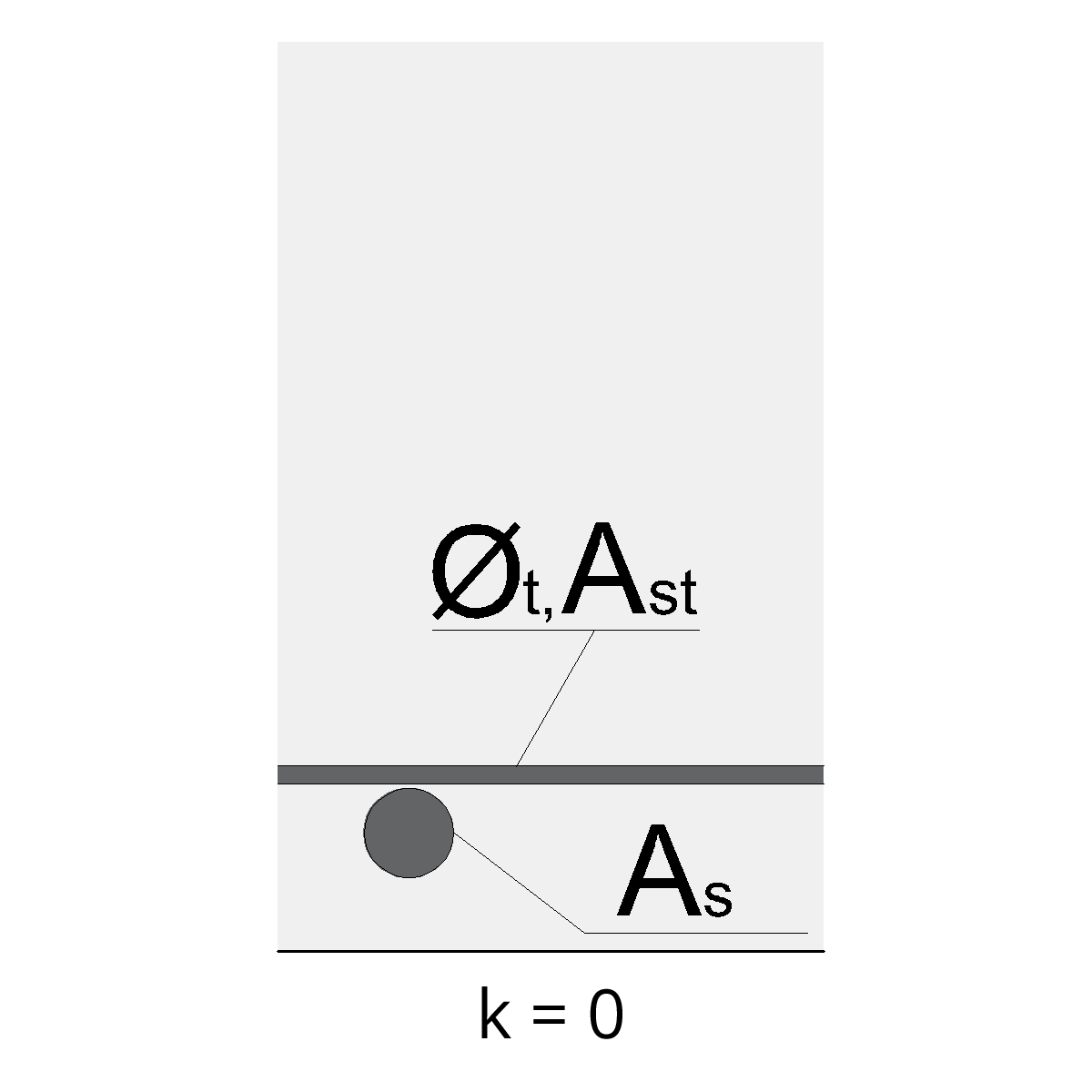
Pour réduire la longueur d’ancrage des aciers d’une poutre, il est fortement recommandé de confiner l’appui avec des cadres.
𝛼4 : Ce coefficient est fixé à 0,7 pour les armatures transversales soudées, indiquant un bon confinement (ex. : présence de treillis soudés) :
Tout type d’ancrage : α4 = 0,7.
𝛼5 : Ce coefficient prend en compte l’effet de la compression transversale sur l’ancrage de la barre :
Tout type d’ancrage : α5 = 1 – 0,04*p et 0,7 ≤ α5 ≤ 1;
p = pression à ELU en Mpa.
Remarque : Pour les barres en compression, tous les coefficients αi sont égaux à 1, sauf α4 qui est fixé à 0,7.
Chaque coefficient αi (pour i de 1 à 5) peut réduire la longueur d’ancrage, mais doit respecter les limites suivantes :
Chaque coefficient αi doit être compris entre 0,7 et 1 : 0.7 ≤ αi ≤ 1.
Le produit des coefficients α2, α3, α5 doit être supérieur ou égal à 0.7 : α2*α3*α5 ≥ 0.7
Le coefficient α4 ne peut pas être cumulé avec α3.
L’Eurocode 2 impose des limites à la valeur de la longueur d’ancrage lbd pour garantir la sécurité et l’efficacité structurelle. La longueur d’ancrage doit être au moins égale à une longueur minimale lb,min : lbd ≥ lb,min.
Pour les barres tendues :
lb,min = max [0,3*lb,rqd ; 10*∅ ; 10 cm];
Pour les barres comprimées :
lb,min = max [0,6*lb,rqd ; 10*∅ ; 10 cm].
Dans le cas des appuis directs (comme les poutres sur les murs), il est possible de considérer lbd inférieur à lb,min si une armature transversale est soudée sur la barre ancrée à l’intérieur de l’appui à une distance de 15 mm.
Les barres qui ont un diamètre important (supérieur à HA 32) doivent être ancrées de la même manière que les barres droites ou à l’aide de manchons.
Ces limitations garantissent que les barres d’armature, qu’elles soient en traction ou en compression, ont une longueur d’ancrage suffisante pour assurer leur adhérence et leur résistance dans le béton.
En appliquant correctement ces coefficients, les ingénieurs peuvent optimiser la longueur d’ancrage nécessaire, ce qui peut conduire à des économies de matériau et de temps tout en maintenant la sécurité et l’efficacité structurelle. Cela permet également d’adapter les calculs d’ancrage à des situations particulières, comme des conditions d’enrobage variables ou des diamètres de barres spécifiques.
Selon l’Eurocode 2, plusieurs critères doivent être respectés pour assurer un ancrage efficace des treillis soudés. Il existe trois méthodes de la vérification de l’ancrage suffisant d’un treillis soudé à l’appui.
Méthode 1 : En ignorant l’existence d’une soudure transversale, on examine un ancrage standard droit en s’assurant que l (longueur d’ancrage) est supérieur ou égal à lbd (longueur d’ancrage de calcul). Si cette condition n’est pas remplie, on a la possibilité d’adopter une longueur d’ancrage forfaitaire déterminée par le coefficient forfaitaire α4.
Méthode 2 : En utilisant le coefficient forfaitaire α4, on s’assure que l est supérieur à so (Débord du fil qui dépasse la soudure, souvent la moitié de l’espace entre les fils transversaux.) + 50 mm et à 0,7 lbd. Si ces conditions ne sont pas remplies, on a la possibilité de déterminer la longueur d’ancrage pour le treillis soudé (TS) en fonction de la résistance de la soudure, en se référant à l’article 8.6 de Eurocode 2.
Méthode 3 : Estimation de la résistance de la soudure.
La capacité de charge que la soudure peut supporter est déterminée par la formule suivante :
FR = min [0.5*As*fyd; (16*As*fcd*∅t)/∅];
Ici, FR représente l’effort que peut reprendre la soudure, As est la section de l’acier, fyd est la limite d’élasticité de l’acier, fcd est la contrainte de calcul du béton, et ∅t est le diamètre d'acier tranversale.
L’effort résiduel, qui est la différence entre l’effort total dans l’acier As*σs et l’effort repris par la soudure FR, doit être repris par une longueur rectiligne l. Par conséquent, il est nécessaire de vérifier l’inégalité suivante :
As*σs - FR ≤ l*ℼ*∅*fbd;
Dans cette formule, σs est la contrainte dans l’acier, ℼ est le nombre pi, ∅ est le diamètre de la barre d’acier, et fbd est la contrainte de calcul du béton en traction. Si cette inégalité est respectée, cela signifie que la soudure est capable de reprendre l’effort résiduel.
Pour plus d’informations sur l’ancrage des treillis soudés, nous vous invitons à consulter les ressources suivantes :
Le document “Ancrage des Treillis Soudés ” disponible sur le site de l’EGF.BTP. Ce document offre une vue détaillée sur le sujet et pourrait être très utile pour approfondir vos connaissances.
La “TS : Note explicative” disponible sur le site de l’ADETS. Cette note explicative fournit des informations supplémentaires qui pourraient compléter votre compréhension de l’ancrage des treillis soudés.
N’hésitez pas à consulter ces documents pour obtenir des informations plus détaillées et précises.