
Ce logiciel en ligne open source permet de dimensionner et de vérifier un poteau en béton armé de section rectangulaire, soumis à une charge verticale centrée, conformément à l’ Eurocode 2 (EN 1992-1-1). Il applique la méthode de la courbure nominale pour le dimensionnement des poteaux élancés, la vérification de leur stabilité structurelle et la détermination de la section d’acier requise.
L’outil génère automatiquement les résultats essentiels : sollicitations internes, descente de charges, vérification de la résistance, quantités de béton et d’acier, ainsi que la disposition des armatures longitudinales et transversales. Les données sont présentées sous forme de tableaux normatifs et de schémas pédagogiques, facilitant leur exploitation en atelier ou sur chantier.
En complément du calcul structurel, l’outil fournit également le ferraillage complet du poteau en béton armé selon l’Eurocode 2 : nomenclature des barres, schémas clairs en plan et en élévation, ainsi qu’un récapitulatif des quantités d’acier et de béton. Cette présentation normalisée facilite la lecture des résultats et prépare directement la fabrication en atelier ou l’assemblage sur chantier.
Conçu pour les ingénieurs, les étudiants en génie civil et les professionnels de la construction, ce logiciel constitue une ressource fiable pour comprendre et appliquer les règles de l’Eurocode 2 au dimensionnement des poteaux en béton armé.
Important : les résultats fournis sont indicatifs et doivent être validés par un bureau d’études spécialisé avant toute mise en œuvre réelle.
Afin de garantir la validité des résultats et la conformité aux prescriptions de l’Eurocode 2, ce logiciel doit être utilisé uniquement dans les cas suivants :
Le calcul d’un poteau en béton armé soumis à une charge centrée est réalisé conformément aux prescriptions de l’Eurocode 2 (EN 1992-1-1), en appliquant la méthode de la courbure nominale (§ 5.8.8). Cette approche permet de vérifier la stabilité et la résistance du poteau en tenant compte de son élancement, de la rigidité de la section et des effets du flambement.
Le dimensionnement comprend la définition des paramètres de projet, la saisie des dimensions géométriques, l’évaluation des charges permanentes et d’exploitation, ainsi que la vérification des conditions d’élancement. Les résultats obtenus conduisent ensuite au calcul de la section d’acier nécessaire et à la validation de la disposition des armatures longitudinales et transversales.
Ce calcul normatif fournit une base fiable et conforme aux exigences de l’Eurocode 2 pour la conception, la vérification et l’optimisation des poteaux en béton armé.
Indiquez les paramètres initiaux de votre projet de construction à l’aide du tableau ci-dessous.
Vous aurez la possibilité de modifier ces valeurs par la suite.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Durée d’utilisation
T
ans
Acier à béton
B
MPa
Resistance du beton à la compression
fck
MPa
Resistance du beton en flexion
fcd = αcc * (fck/ɣc)
MPa
Resistance moyenne du en compression
fcm = fck + 8MPa
MPa
Resistance du beton en traction
fctk, 0.05
MPa
Contrainte de traction axiale de calcul
fctd = αct * (fctk,0.05 / ɣc)
MPa
Module d'élasticité moyen du béton
Ecm = 22 × (fcm / 10)0.3
GPa
Déformation relative ultime en compression :
εcu2 = 3.5x10-3 si classe < C55;
‰
Dimension nominale du plus gros granulat:
Dmax
mm
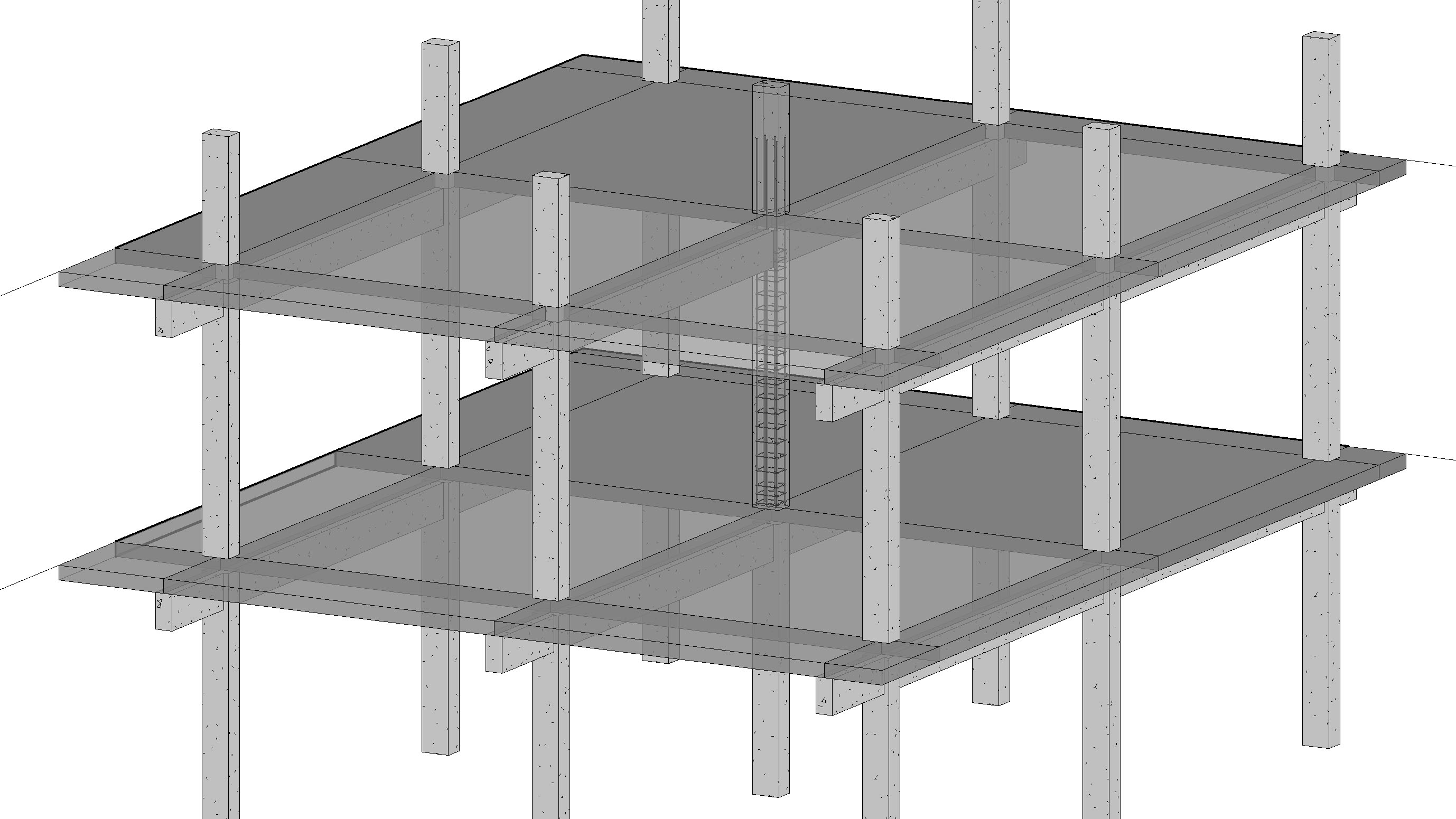
Référez-vous aux schémas présentés ci-dessous pour une saisie précise des données : définissez les dimensions initiales du poteau à calculer (section rectangulaire ou carrée), la hauteur du poteau (correspondant à la hauteur libre entre deux planchers porteurs successifs), renseignez les caractéristiques des poutres situées au-dessus et au-dessous du poteau — en incluant, si elles existent, les charges permanentes des murs agissant sur les poutres du niveau supérieur — et indiquez les dimensions des dalles supérieures et inférieures, si elles sont présentes. Les dimensions du poteau pourront être ajustées par la suite en fonction des résultats obtenus.
Notre outil effectue automatiquement le calcul des sollicitations conformément aux principes de l’Eurocode 2, en intégrant la descente de charges verticales transmises par les dalles et les poutres, ainsi que les moments fléchissants appliqués au poteau.
👉 (Cliquez sur l’image pour agrandir.)
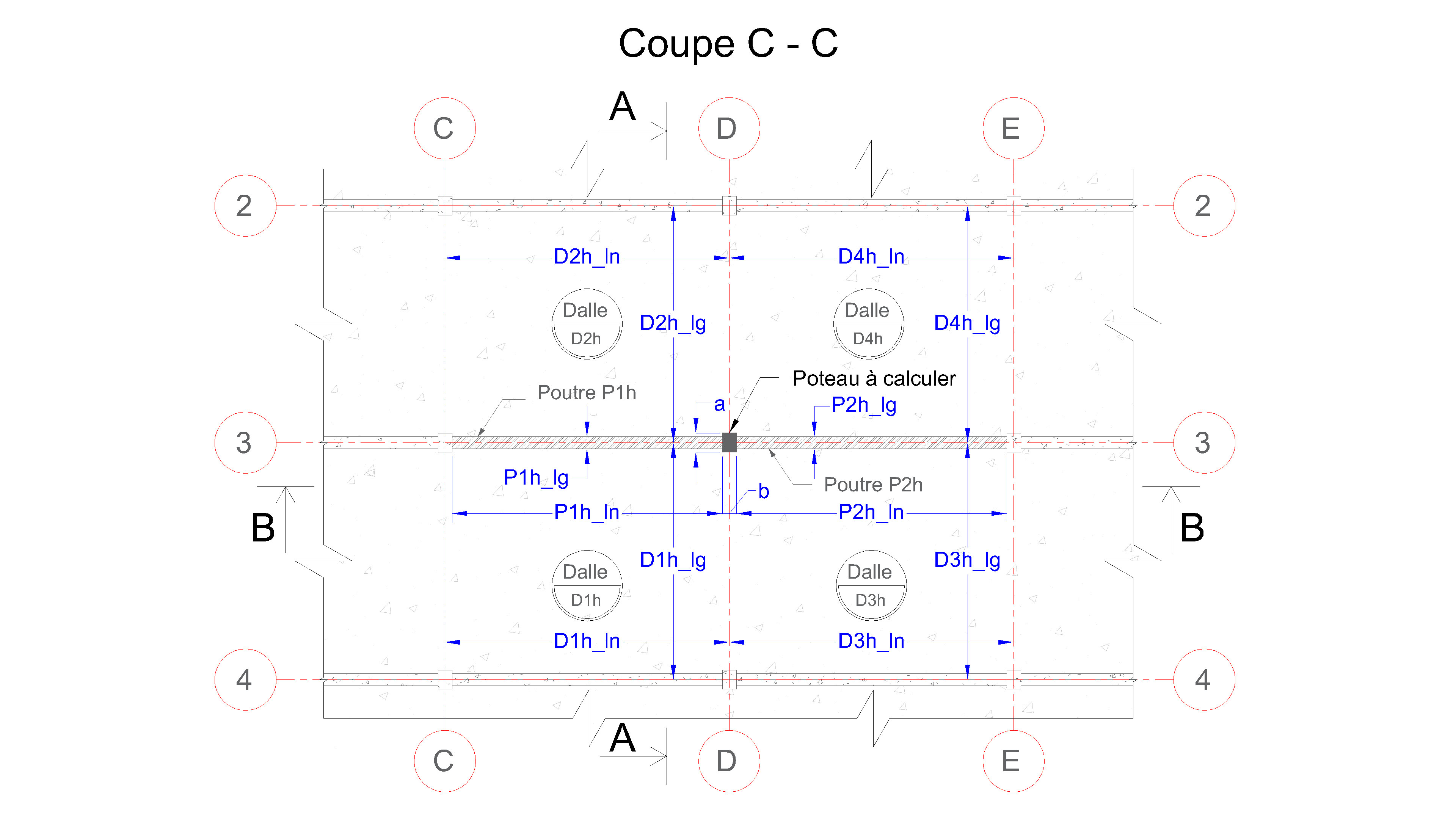
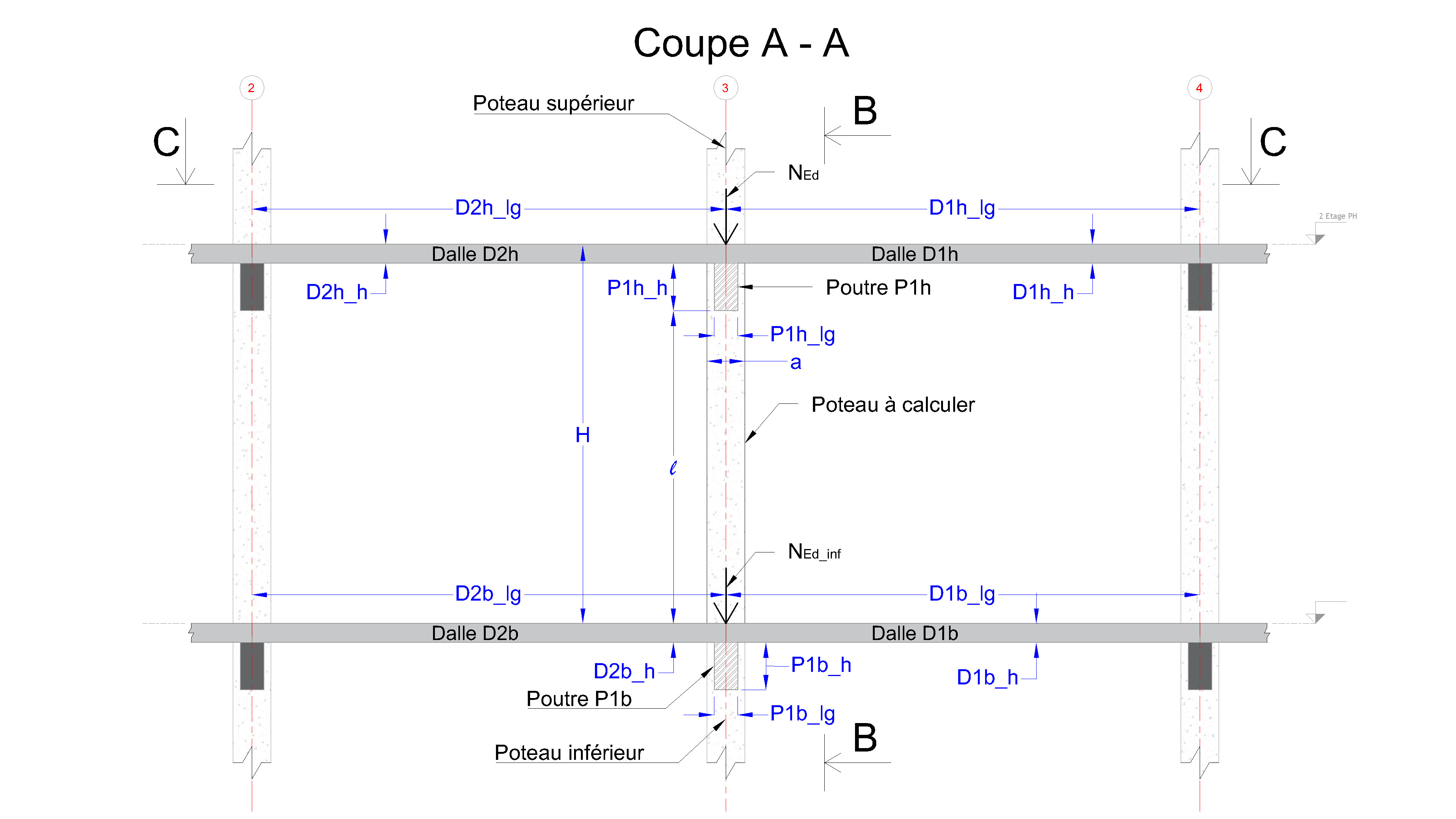
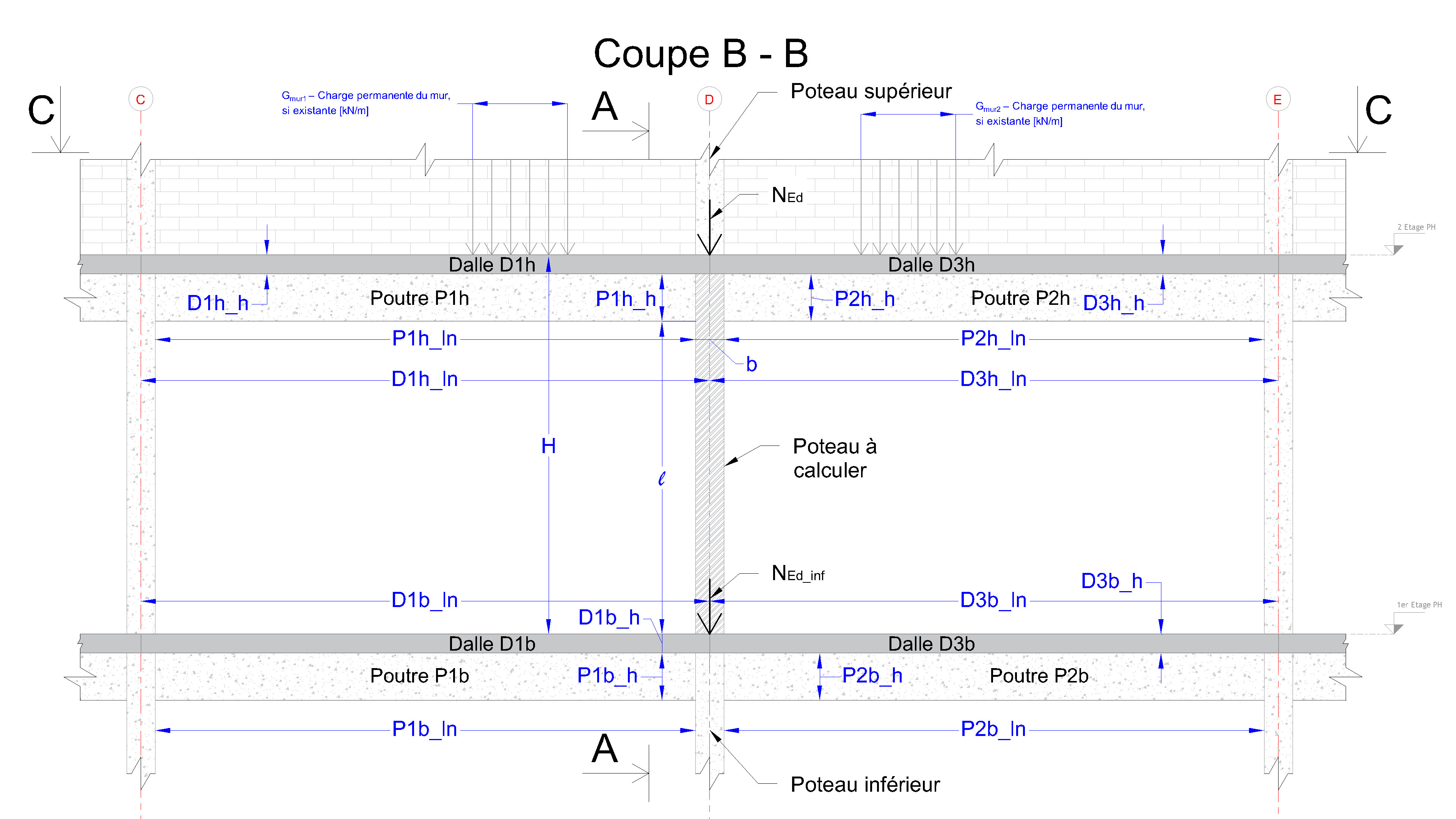
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Longueur
a
m
Largeur
b
m
Hauteur du poteau
H
m
Un élément est considéré comme un poteau s’il respecte simultanément les trois conditions géométriques suivantes :
➤ Section rectangulaire équilibrée : l’un des côtés de la section est supérieur ou égal à l’autre ;
➤ Élancement modéré : le côté le plus long ne dépasse pas quatre fois le côté le plus court ;
➤ Hauteur suffisante : la hauteur de l’élément est supérieure à trois fois le côté le plus long.
🔎 Exemple d’application : si b est le côté le plus court :
Ces critères permettent de différencier un poteau d’un mur porteur mince ou d’une poutre verticale.
Si une ou plusieurs conditions ne sont pas remplies, il convient d’adapter les dimensions afin de respecter les prescriptions de l’Eurocode 2 pour la conception des poteaux.
Dans le tableau ci-dessous :
| Condition | Valeur calculée | Résultat |
|---|---|---|
| Longueur (a) ≥ 0,15 m (selon EC2) | 0.40 ≥ 0.15 | OK |
| Largeur (b) ≥ 0,15 m (selon EC2) | 0.40 ≥ 0.15 | OK |
| Longueur (a) ≥ Largeur (b) | 0.40 ≥ 0.40 | OK |
| Longueur (a) < 4 × Largeur (b) | 0.40 < 1.60 | OK |
| Hauteur (H) > 3 × Longueur (a) | 4.00 > 1.20 | OK |
| Conclusion : L’élément est un poteau | ✔️ | OUI |
Pour poursuivre le calcul du ferraillage conformément à l’Eurocode 2, veuillez renseigner les dimensions des éléments structurels liés au poteau étudié : poteau supérieur (si présent), poteau inférieur, deux poutres supérieures, deux poutres inférieures, dalles supérieures (si présentes) et dalles inférieures (si présentes).
Ces informations permettront à l’outil de :
Remarque :
Dans le cadre du calcul du poteau, le moment quadratique minimal des éléments connectés est retenu afin de représenter le cas défavorable.
Si un élément structurel n’existe pas, veuillez saisir la valeur 0 dans tous ses champs correspondants.
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Longueur (m) | asup | |
| Largeur (m) | bsup | |
| Hauteur (m) | Lsup | |
| Moment quadratique (m⁴) | Isup = ab³/12 | 0.0021 |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Longueur (m) | ainfr | |
| Largeur (m) | binfr | |
| Hauteur (m) | Linfr | |
| Moment quadratique (m⁴) : | Iinfr = ab³/12 | 0.0021 |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Longueur (m) | P1hln | |
| Largeur (m) | P1hlg | |
| Hauteur (m) | P1hh | |
| Volume (m³) | V = L × b × h | 0.7 |
| Poids propre G (kN) | G = V × 25 kN/m³ | 17.50 |
| Moment quadratique (m⁴) | IP1h = b × h³ / 12 | 0.0007 |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Longueur (m) | P2hln | |
| Largeur (m) | P2hlg | |
| Hauteur (m) | P2hh | |
| Volume (m³) | V = L × b × h | 0.7 |
| Poids propre G (kN) | G = V × 25 kN/m³ | 17.50 |
| Moment quadratique (m⁴) | IP2h = b × h³ / 12 | 0.0007 |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Longueur (m) | P1bln | |
| Largeur (m) | P1blg | |
| Hauteur (m) | P1bh | |
| Volume (m³) | V = L × b × h | 0.7 |
| Poids propre G (kN) | G = V × 25 kN/m³ | 17.50 |
| Moment quadratique (m⁴) | IP1b = b × h³ / 12 | 0.0007 |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Longueur (m) | P2bln | |
| Largeur (m) | P2blg | |
| Hauteur (m) | P2bh | |
| Volume (m³) | V = L × b × h | 0.7 |
| Poids propre G (kN) | G = V × 25 kN/m³ | 17.50 |
| Moment quadratique (m⁴) | IP2b = b × h³ / 12 | 0.0007 |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Largeur (m) | D1hlg | |
| Épaisseur (m) | D1hh |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Largeur (m) | D2hlg | |
| Épaisseur (m) | D2hh = D1hh |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Largeur (m) | D3hlg | |
| Épaisseur (m) | D3hh |
| Appellation | Symbole / Formule | Valeur |
|---|---|---|
| Largeur (m) | D4hlg | |
| Épaisseur (m) | D4hh = D3hh |
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Épaisseur dalle inférieure
D1bh / D2bh
m
À renseigner si cette dalle existe dans votre structure.
Le calcul de la longueur de flambement L₀ d’un poteau soumis à une compression axiale (méthode de la courbure nominale – EC2) repose sur l’évaluation des conditions de liaison à ses extrémités.
Pour cela, deux coefficients de souplesse, notés k₁ (extrémité supérieure) et k₂ (extrémité inférieure), sont utilisés. Ils expriment la rigidité relative des éléments structurels connectés au poteau et varient généralement entre 0 (encastrement parfait) et 1 (appui simple articulé).
Renseignez les éléments connectés au poteau :
Contrairement aux méthodes simplifiées (telles que L₀ = 0,7L, L ou 2L), cette approche offre une estimation plus réaliste car elle prend en compte la configuration réelle du poteau dans l’ouvrage.
Moment quadratique calculé pour la direction la plus défavorable (axe de moindre inertie), conformément aux prescriptions de l’EC2 lorsque la direction de flambement n’est pas déterminée.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Distance libre
l
m
Hauteurs d’appui en haut
hsup
m
Hauteurs d’appui en bas
hinf
m
Hauteur utile
L = l + hsup/2 + hinf/2
m
Moment quadratique
Ic = a·b³/12
m⁴
Section béton
Ac = a*b
m²
Coefficient de souplesse en tête du poteau
k1 =
[ (Ic/L) + (Isup/Lsup) ] /
[ 3·(Ip1/Lp1) + 3·(Ip2/Lp2) ]
-
Coefficient de souplesse à la base du poteau
k2 =
[ (Ic/L) + (Iinfr/Linfr) ] /
[ 3·(Ip3/Lp3) + 3·(Ip4/Lp4) ]
-
Longueur de flambement
L0 = 0.5·L·√( [1 + k1 / (0.45 + k1)] · [1 + k2 / (0.45 + k2)] )
m
Regroupement de l’ensemble des paramètres nécessaires au calcul des charges appliquées au poteau à dimensionner, conformément aux prescriptions des Eurocodes.
Un coefficient de continuité peut être appliqué lorsque le poteau est proche d’une rive et que la structure comporte plusieurs travées consécutives, afin de tenir compte de la redistribution des efforts.
👉 L’ensemble de ces données est automatiquement intégré dans le calcul pour déterminer l’effort axial de dimensionnement NEd, conformément aux Eurocodes EN 1990, EN 1991 et EN 1992.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Effort axial appliqué sur le poteau
(si exist)
NEd
kN
Saisir NEd (ELU) issu de la descente de charges des niveaux supérieurs.
Mur sur P1h
(si exist)
Gmur1
kN/m
Saisir la valeur « G (kN/m) » depuis l’outil descente de charge des murs .
Mur sur P2h
(si exist)
Gmur2
kN/m
Saisir la valeur « G (kN/m) » depuis l’outil descente de charge des murs .
Mur sur P1b
(si exist)
Gmur1,infr
kN/m
Saisir la valeur « G (kN/m) » depuis l’outil descente de charge des murs .
Mur sur P2b
(si exist)
Gmur2,infr
kN/m
Saisir la valeur « G (kN/m) » depuis l’outil descente de charge des murs .
Choisissez ci-dessous le type de revêtement de sol ou de surface appliqué sur votre dalle en béton. La valeur exprimée en kN/m² sera intégrée au calcul de la charge totale permanente de la structure. Il est possible d’ajouter plusieurs revêtements si nécessaire pour obtenir une estimation plus précise.
📄 Pour plus de détails, consultez notre tableau PDF des poids surfaciques des revêtements , qui répertorie les valeurs de charge pour les principaux matériaux (carrelage, parquet, chape, moquette, etc.) avec explications.
| Revêtement | Valeur | Unité |
|---|---|---|
| 0.25 | kN/m² | |
| Total Grev | 0.25 | kN/m² |
Si votre structure comporte un plancher inférieur (étage bas) avec un revêtement de sol, saisissez sa valeur en kN/m². Cette charge sera ajoutée dans le calcul des moments et efforts du poteau. Laisser à 0 si aucun revêtement n’est présent.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Revêtement étage inférieur
Grev,b
kN/m²
Indiquez ici le poids surfacique du revêtement de sol de l’étage inférieur.
Sélectionnez la charge d’exploitation adaptée à l’usage de votre plancher. Les valeurs, exprimées en kN/m², servent à déterminer la charge que la structure devra supporter et sont basées sur les valeurs officielles de l’Eurocode EN 1991-1-1 ainsi que de sa version française (Annexe nationale 6.2 F2).
📄 Pour en savoir plus, consultez notre tableau PDF des charges d’exploitation par catégorie de bâtiment, qui présente les valeurs officielles selon l’usage (habitation, bureaux, lieux publics, commerces, etc.) avec des exemples et explications simples.
| Catégorie d’usage | qₖ (kN/m²) | Unité |
|---|---|---|
| 1.50 | kN/m² | |
| Charge d’exploitation qₖ | 1.50 | kN/m² |
| Condition du poteau | Coefficient |
|---|---|
| 1.00 | |
| Coefficient de continuité appliqué kcont | 1.00 |
La descente de charges détermine :
La charge totale appliquée au poteau est calculée selon la combinaison réglementaire (EN 1990 – Eurocode : Bases de calcul des structures) :
NEd = NEd,sup + kcont × [1.35 × ΣG + 1.5 × ΣQ]
où ΣG et ΣQ sont les sommes des charges permanentes et d’exploitation transmises par l’ensemble des éléments connectés au poteau (réf. EN 1991 – Eurocode 1).
Si le poteau est proche d’une rive et que le plancher ou la poutre est continu sur ≥ 3 travées, un coefficient de continuité (1.10 ou 1.20) est appliqué pour tenir compte de la redistribution des efforts (EN 1992-1-1 – Eurocode 2).
👉 Résultat final : les valeurs indiquées dans le tableau représentent les charges concentrées (NEd) au droit du poteau, transmises à l’étage inférieur (en kN).
| Appellation | Symbole / Formule | Valeur | Unité |
|---|---|---|---|
| Effort axial appliqué sur le poteau | NEd (Étages supérieurs) = NEd,sup | 0 | kN |
| Poteau (G) | Gp = 25 kN/m³ × a × b × (H − hdalles_max) | 15.20 | kN |
| Poutre P1h (G) | GP1h = 25 kN/m³ × (P1hln ⁄ 2) × P1hlg × P1hh | – | kN |
| Mur sur P1h (G) | Gmur,P1h = Gmur1,lin × (P1hln ⁄ 2) | – | kN |
| Poutre P2h (G) | GP2h = 25 kN/m³ × (P2hln ⁄ 2) × P2hlg × P2hh | – | kN |
| Mur sur P2h (G) | Gmur,P2h = Gmur2,lin × (P2hln ⁄ 2) | – | kN |
| Dalle D1h (G) | GD1h = 25 kN/m³ × (D1hln ⁄ 2) × (D1hlg ⁄ 2) × D1hh + ((D1hln ⁄ 2) × (D1hlg ⁄ 2) × Grev) | – | kN |
| Dalle D1h (Q) | QD1h = (D1hln ⁄ 2) × (D1hlg ⁄ 2) × q | – | kN |
| Dalle D2h (G) | GD2h = 25 kN/m³ × (D2hln ⁄ 2) × (D2hlg ⁄ 2) × D2hh + ((D2hln ⁄ 2) × (D2hlg ⁄ 2) × Grev) | – | kN |
| Dalle D2h (Q) | QD2h = (D2hln ⁄ 2) × (D2hlg ⁄ 2) × q | – | kN |
| Dalle D3h (G) | GD3h = 25 kN/m³ × (D3hln ⁄ 2) × (D3hlg ⁄ 2) × D3hh + ((D3hln ⁄ 2) × (D3hlg ⁄ 2) × Grev) | – | kN |
| Dalle D3h (Q) | QD3h = (D3hln ⁄ 2) × (D3hlg ⁄ 2) × q | – | kN |
| Dalle D4h (G) | GD4h = 25 kN/m³ × (D4hln ⁄ 2) × (D4hlg ⁄ 2) × D4hh + ((D4hln ⁄ 2) × (D4hlg ⁄ 2) × Grev) | – | kN |
| Dalle D4h (Q) | QD4h = (D4hln ⁄ 2) × (D4hlg ⁄ 2) × q | – | kN |
| Charge totale | NEd = NEd, sup + kcont × [1.35 × ΣG + 1.5 × ΣQ] | 3600.27 | kN |
L’élancement d’un poteau est un indicateur de sa sensibilité au flambement. Il se calcule à partir de la longueur de flambement L0, de l’inertie Ic et de l’aire de la section Ac.
👉 En comparant l’élancement réel λ avec l’élancement limite λlim (selon l’EN 1992-1-1, §5.8.3), on vérifie si les effets du flambement doivent être pris en compte dans le dimensionnement.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
L’élancement de poteau
λ = L0 / √(Ic/Ac)
-
Élancement du poteau (selon EN 1992-1-1, §5.8.3.2(1))
Coefficient A
A = 1 / (1 + 0.2 × φef)
-
φef = coefficient de fluage effectif (si inconnu, A = 0,7 par défaut)
Coefficient B
B = √(1 + 2 × ω)
-
ω = paramètre lié à la distribution des moments (si inconnu, B ≈ 1,1)
Coefficient C
C = 1.7 − rm
-
rm = M01 / M02 (si inconnu, C = 0,7) — voir EN 1992-1-1 §5.8.3.1
Effort normal relatif n
n = NEd / (Ac × fcd)
-
Calculé avec les valeurs de charge et béton
Élancement limite λlim
λlim = 20 × A × B × C / √n
-
Limite d’élancement selon EN 1992-1-1, §5.8.3.1(2)
Vérification obligatoire selon l’Eurocode 2 (EN 1992-1-1, §5.8.3). Les conditions ci-dessus déterminent si les effets du second ordre peuvent être négligés, doivent être pris en compte (méthode de la courbure nominale), ou nécessitent une analyse plus avancée. Se référer également à l’Annexe nationale applicable.
| Condition | Valeur calculée | Vérification | Interprétation |
|---|---|---|---|
| λ ≤ λlim | 0 ≤ 0 | ❌ | |
| λ ≤ 200 | 0 ≤ 200 | ❌ |
Conclusion : …
Conformément à l’Eurocode 2, lorsque le rapport d’élancement λ d’un poteau est supérieur à la valeur limite λlim, les moments de premier ordre doivent être complétés par un moment additionnel.
Ce calcul prend en compte l’augmentation des moments de flexion due aux effets de flambement, en fonction de la géométrie de la section, de la charge axiale appliquée et des conditions de flambement. Il permet de garantir que la section armée reste sécurisée et conforme aux exigences de l’Eurocode, même dans les cas où la déformation due au flambement amplifie sensiblement les sollicitations.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Limite élastique de l’acier
fyk
MPa
Résistance de l'acier
fyd = fyk / γs
MPa
γs = 1.15 (Coefficient de sécurité)
Déformation de calcul de l'acier
εyd = fyd / Es
‰
Es = 200 000 MPa
Dimension de la section (axe faible)
heff
m
heff = b si L₀ / (b / √12) ≥ L₀ / (a / √12) ; sinon heff = a
Hauteur utile de la section (estimation)
destimé = heff - 40mm
m
Hypothèse de pré-dimensionnement avec enrobage + demi-barre
Hauteur utile de la section (calcul précis)
d = heff - (cnom + ∅l/2 + ∅tr)
m
Valeur provisoire à ajuster après choix des armatures. ∅l = diamètre des barres (à déterminer), ∅tr = diamètre des cadres.
Courbure de base
1/r₀ = εyd/(0,45 × d)
1/m
Coefficient de correction (effet de l’effort normal)
Kr = (νu - n) / (νu - nbal) ≥ 1
νu = 1 + ω ; ω = As × fyd / (Ac × fcd)
n = NEd / (Ac × fcd) ; nbal = 0.4
-
As inconnu : Kr fixé à 1 (cas défavorable). Cette valeur pourra être ajustée après le calcul de As.
Coefficient β
β = 0,35 + fck/200 - λ/150
-
Coefficient de fluage
Kφ = 1 + β × φef ≥ 1
-
Coefficient de fluage effectif φef = 2,0 (valeur courante dans les cas standards – béton courant, ambiance normale)
Courbure de calcul
1/r = Kr×Kφ×(1/r₀)
1/m
Excentricité du second ordre
e2 = (1/r) × L₀²/c
m
c = π² ≈ 10 (pour poteau bi-articulé)
Excentricité initiale
e0 = max ( L0/400 ; h/30 ; 0.02 )
m
Excentricité initiale selon EN 1992‑1‑1 §5.2.1(2) pour poteaux élancés.
Moment en tête de poteau (1er ordre)
Mhaut
kNm
Moment nodal de premier ordre obtenu par la méthode de distribution (Hardy-Cross) au niveau supérieur.
Moment en pied de poteau (1er ordre)
Mbas
kNm
Moment nodal de premier ordre obtenu par la méthode de distribution (Hardy-Cross) au niveau inférieur.
Moment M01
M01 = min[|Mhaut| ; |Mbas|] + NEd · e0
kNm
Moment de référence, basé sur la plus petite extrémité, augmenté de l’effet de l’imperfection initiale e0 selon §5.2.1, §5.2.7, §6.1.4 de EC2 et l’ANF.
Moment M02
M02 = max[|Mhaut| ; |Mbas|] + NEd·e0
kNm
Moment de référence, basé sur la plus grande extrémité, augmenté de l’effet de l’imperfection initiale e0 selon §5.2.1, §5.2.7, §6.1.4 de EC2 et l’ANF.
Moment équivalent
M0,Ed = max [ 0.6·M02 + 0.4·M01 ; 0.4·M02 ]
|M02| ≥ |M01|
kNm
Moment de calcul de premier ordre équivalent selon l’Eurocode 2 (EN 1992-1-1 §5.8.8.2), basé sur les moments extrêmes corrigés.
Moment M2 (imperfection secondaire)
M2 = NEd · e2
kNm
Moment additionnel dû à l’imperfection e2 appliquée au poteau selon EC2.
Moment final de calcul
MEd = max [ M02 ; M0,Ed + M2 ; M01 + 0.5·M2 ; NEd·e0,min ]
kNm
Moment final de calcul obtenu par la méthode de la courbure nominale
selon EN 1992-1-1 (§5.8.3.2 et §5.8.8.2)
e0,min = 0.02m - valeur fixée par l’ANF.
Selon l’EN 1992‑1‑1, la section d’armatures longitudinales d’un poteau en béton armé As doit être comprise entre As,min et As,max. La méthode itérative consiste à déterminer la position de la fibre neutre x et on vérifie l’équilibre axial et flexionnel : NRd(x,As) ≥ NEd et MRd(x,As) ≥ MEd.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Acier minimal
As,min = max(0.1·NEd/fyd ; 0.002·Ac)
cm²
Valeur minimale imposée par EN 1992-1-1 §9.5.2
Acier maximal
As,max = 0.04 · Ac
cm²
Limite de pourcentage d’armatures longitudinales selon EN 1992-1-1 §9.5.2.
Fibre neutre
x
mm
0 < x ≤ h
h = grand côté.
Section d’acier trouvé
As,trouvé
cm²
Vérifier As ≤ As,min
et As ≥ As,max
Déformation acier comprimé
εs,comp(x) = εcu · (x − d′) / x
–
Déformation acier tendu
εs,trac(x) = εcu · (x − d) / x
–
Contrainte acier comprimé
σs,comp(x) = sign(εs,comp) · min(Es·|εs,comp| ; fyd)
MPa
Es = 200000 MPa.
Contrainte acier tendu
σs,trac(x) = sign(εs,trac) · min(Es·|εs,trac| ; fyd)
MPa
Es = 200000 MPa.
Force d’acier en traction
Fs,trac = As/2 · σs,trac
kN
Force d’acier en compression
Fs,comp = As/2 · σs,comp
kN
Capacité portante du béton seul
Cc = η · fcd · b · x
kN
Pour fck ≤ 50 MPa : η = 1.0.
b = petit côté
Effort normal résistant
NRd(x) = Cc(x) + Fs,comp + Fs,trac
kN
NRd(x) = NEd par bisection pour obtenir x.
Moment résistant
MRd(x) = Cc(x)·(d − λx/2) + Fs,comp·(d − d′)
kNm
λ = 0.8 pour fck ≤ 50.
Section d’acier finale
As ∈ [As,min, As,max]
cm²
pour le x correspondant, MRd(x) ≥ MEd.
Les vérifications de la section d’armatures longitudinales d’un poteau en béton armé, conformément à l’EN 1992‑1‑1, incluent la résistance axiale, la résistance en flexion, ainsi que le respect des limites minimale et maximale d’acier.
Ce contrôle garantit la sécurité et la performance structurale du poteau.
| Condition | Valeur calculée | Vérification | Interprétation |
|---|---|---|---|
| Vérification axiale : NEd ≤ NRd | 0 ≤ 0 | ❌ | |
| Vérification flexionnelle : MEd ≤ MRd | 0 ≤ 0 | ❌ | |
| Vérification de l’acier minimal : As,calc ≥ As,min | 0 ≥ 0 | ❌ | |
| Vérification de l’acier maximal : As,calc ≤ As,max | 0 ≤ 0 | ❌ |
Conclusion : …
Les barres longitudinales assurent la résistance principale du poteau aux efforts de compression et de flexion. Selon l’Eurocode 2, elles doivent être disposées de manière symétrique afin de garantir un comportement mécanique régulier et d’éviter les concentrations de contraintes.
La disposition minimale comprend quatre barres disposées aux angles. Des barres supplémentaires, si nécessaires, sont réparties uniformément le long des faces, dans le respect des espacements minimaux et maximaux prescrits par la norme. Conformément à l’Eurocode 2, le diamètre minimal d’une barre longitudinale dans un poteau est de 8 mm.
Le logiciel détermine automatiquement la configuration optimale : nombre total de barres, répartition par face et diamètre des armatures. La sélection est effectuée sur la base des armatures HA B500 couramment commercialisées en France, en s’appuyant sur le tableau des sections d’aciers pour béton armé.
| Position | Nombre | Diamètre | Espacement | Section | Remarques |
|---|---|---|---|---|---|
| Barres d’angles | 4 | ||||
| Barres sur côté a (aW/aE) | |||||
| Barres sur côté b (bN/bS) | |||||
| Total | ∅cadres | - |
La vérification de la disposition des armatures longitudinales dans un poteau en béton armé, selon l’EN 1992‑1‑1 (Eurocode 2), inclut le respect des taux minimaux et maximaux d’acier, le contrôle des espacements libres entre les barres longitudinales (distance nette entre aciers) et la vérification des diamètres minimaux prescrits pour les barres principales et les cadres.
Ces contrôles garantissent la compacité du ferraillage, la durabilité de l’ouvrage et la sécurité structurale du poteau, en assurant sa conformité aux prescriptions normatives.
| Condition | Valeur calculée | Vérification | Interprétation |
|---|---|---|---|
| Acier minimal : As,total ≥ As,min | 0 ≥ 0 | ❌ | |
| Acier maximal : As,total ≤ As,max | 0 ≤ 0 | ❌ | |
| Espacement minimal : sl,min = max (20, ∅l, Dmax +5mm) : sa ≥ sl,min et sb ≥ sl,min |
0 mm | ❌ | |
| Espacement maximal : sl,max = min (a, b, 400mm) : sa ≤ smax et sb ≤ smax |
0 mm | ❌ | |
| Diamètre minimal barres principales : ∅l ≥ ∅min = 8 mm | 0 mm | ❌ | |
| Diamètre cadres / étriers : ∅tr ≥ ∅tr,min = max(6 mm ; ¼ ∅l) | 0 mm | ❌ |
Conclusion : …
L = H + l0,
avec l0 = α6⋅lbd, α6 =1.5 (barres en compression).
Le calcul des valeurs détaillées de lbd, l0 et des coefficients α est présenté dans le tableau de calcul ci‑dessous.
Dans le cas d’un poteau courant, les coefficients α1, α2, α3 et α5 sont égaux à 1, car aucune condition particulière (crochets, soudure, réduction de contrainte ou confinement spécial) ne s’applique.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Contrainte ultime d’adhérence de calcul
fbd = 2.25×η1×η2×fctd
MPa
Longueur d’ancrage de base théorique
lb,rqd = (∅l/4)×(σsd/fbd)
cm
Longueur d'ancrage de calcul
lbd = α1 × α2 × α3 × α5 × lb,rqd
cm
Longueur d'ancrage minimale
lb,min = max [0.3×lb,rqd; 10*∅l; 100mm]
cm
Longueur de recouvrement
l0 = α6 × lbd
cm
Longueur barres longitudinales
L = H + l0
cm


Dans le dimensionnement des poteaux en béton armé, l’Eurocode 2 fixe des prescriptions précises pour la mise en place des armatures transversales (cadres et épingles).
Espacement maximal des cadres :
smax = min(20·∅l,min ; 400 mm ; a)
où a est le plus petit côté de la section du poteau.
Réduction d’espacement en zones critiques :
L’espacement maximal doit être réduit à smax,réduit = 0.6·smax :
Selon l’Eurocode 2, les armatures transversales doivent densifier les barres longitudinales aux extrémités des poteaux (pied et tête). La zone correspondant à la retombée de la poutre et de la dalle présente toutefois des contraintes pratiques, car les cadres peuvent gêner la mise en place du ferraillage des poutres.
Dans cette zone, les barres longitudinales doivent être maintenues par des cadres espacés selon smax,réduit = 0,6·smax. Ces cadres doivent pouvoir être installés en dernier, directement dans le coffrage, après la mise en place des autres armatures, garantissant ainsi leur maintien sans gêner le reste du ferraillage.
Cette approche assure la sécurité du poteau tout en facilitant le montage des armatures des poutres et dalles.
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Longueur de recouvrement
lrec
m
Longueur de recouvrement des barres venant du poteau inférieur.
Espacement maximal des cadres
smax = min(20·∅l ; 400 mm ; a)
cm
a = plus petit côté de la section du poteau
Espacement max réduit en zones critiques
smax,réduit = 0.6·smax
cm
Applicable aux extrémités des poteaux, aux retombées de poutres et à la zone de recouvrement.
Hauteur utile de la section (réel)
d = heff - (cnom + ∅l/2 + ∅tr)
m
Ajustez cette valeur dans le tableau avec destimé afin d’obtenir des résultats plus précis.
Selon l’Eurocode 2 (EN 1992-1-1, § 9.5.3), lorsque l’écartement entre deux barres longitudinales d’angle dépasse 150 mm, des épingles (cadres intermédiaires) doivent être ajoutées pour assurer le maintien des barres de face et le confinement du béton.
| Face du poteau | Nombre de barres (hors angles) | Espacement (axes, angles inclus) | Épingles requises | Ø Épingles | Longueur |
|---|---|---|---|---|---|
| Face a (aW/aE) | |||||
| Face b (bN/be) |
| Zone | Hcalc | smax/réduit | ncadres | sréel | Hréelle |
|---|---|---|---|---|---|
| Retombée | |||||
| Tête | |||||
| Centrale | |||||
|
Pied (Recouvrement) |
60 (40) |
9 (9) |
2 (4) |
9 (7) |
18 |
| TOTAL |
400 |
– |
18 |
– |
400 |
|
2 | 2×16 | 10×28 | 18 | 3×16 | 16 | 4 |
|
|
Longueur total |
|
|
Total cadres |
|
|
Épingles côté a |
|
|
Épingles côté b |
|
Appellation
Symbole / Formule
Valeur
Unité
Remarques
Diamètre de mandrin (cadres)
Dmandr = 4 × ∅tr
cm
Retour de cadre (135°)
lR(135) = max(5 × ∅tr ; 5 cm)
cm
Retour d’épingle (90°)
lR(90) = max(10 × ∅tr ; 7 cm)
cm
Le ferraillage complet d’un poteau en béton armé, établi à partir des résultats de calcul, se compose de :
Ce ferraillage est prêt pour la fabrication en atelier d’armatures ou pour l’assemblage directement sur chantier.
ℹ. Cliquez sur l’image indiquée dans « Forme / Schéma » pour l’afficher en détail.
| Rep. | Barre (B500B) | Lg dév. (cm) | Détails de façonnage (cm) | Forme / Schéma |
|---|---|---|---|---|
| 1 | 4HA16 | 280 |

|
|
| 1a | 4HA16 | 280 |

|
|
| 1b | 4HA16 | 280 |

|
|
| 2 | 4HA16 | 280 |
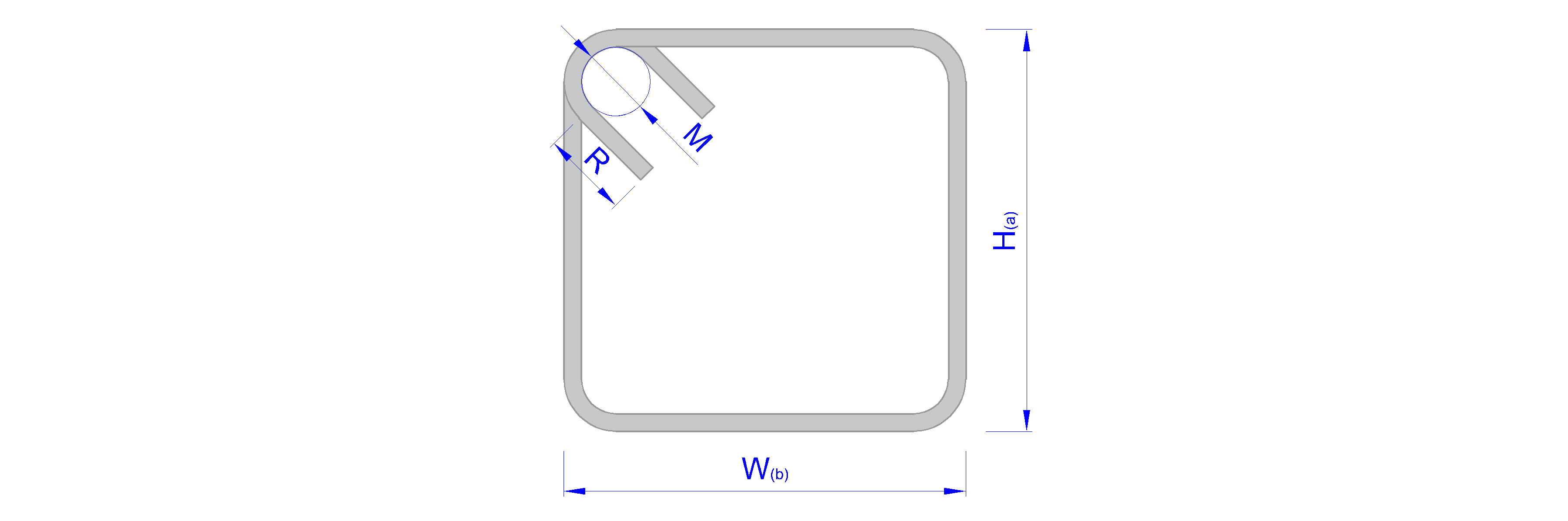
|
|
| 3* | 4HA16 | 280 |

|
|
| 4 | 4HA16 | 280 |
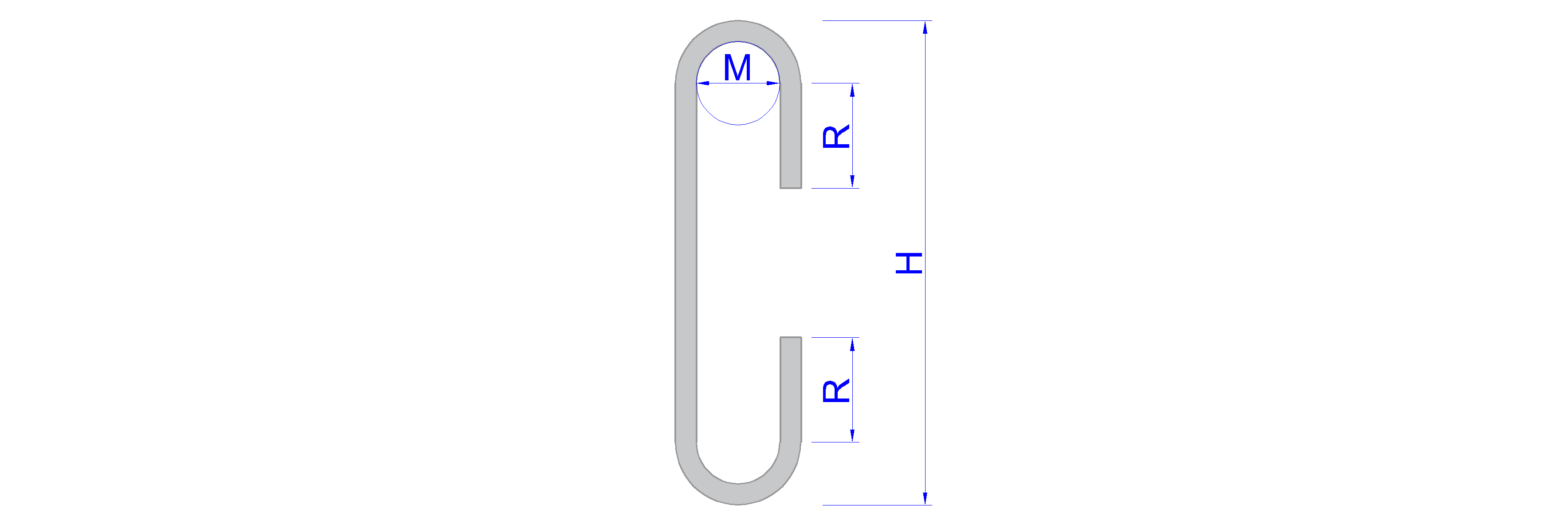
|
|
| 5 | 4HA16 | 280 |

|
|
| 6* | 4HA16 | 280 |

|
|
| 7* | 4HA16 | 280 |

|
|
| Béton : C25/30 ; Acier : HA B500B ; Enrobage : 2,5 cm | ||||
* Ne pas souder ; mise en place et ligature à réaliser sur chantier, afin de permettre l’assemblage correct avec le ferraillage des poutres et dalles.
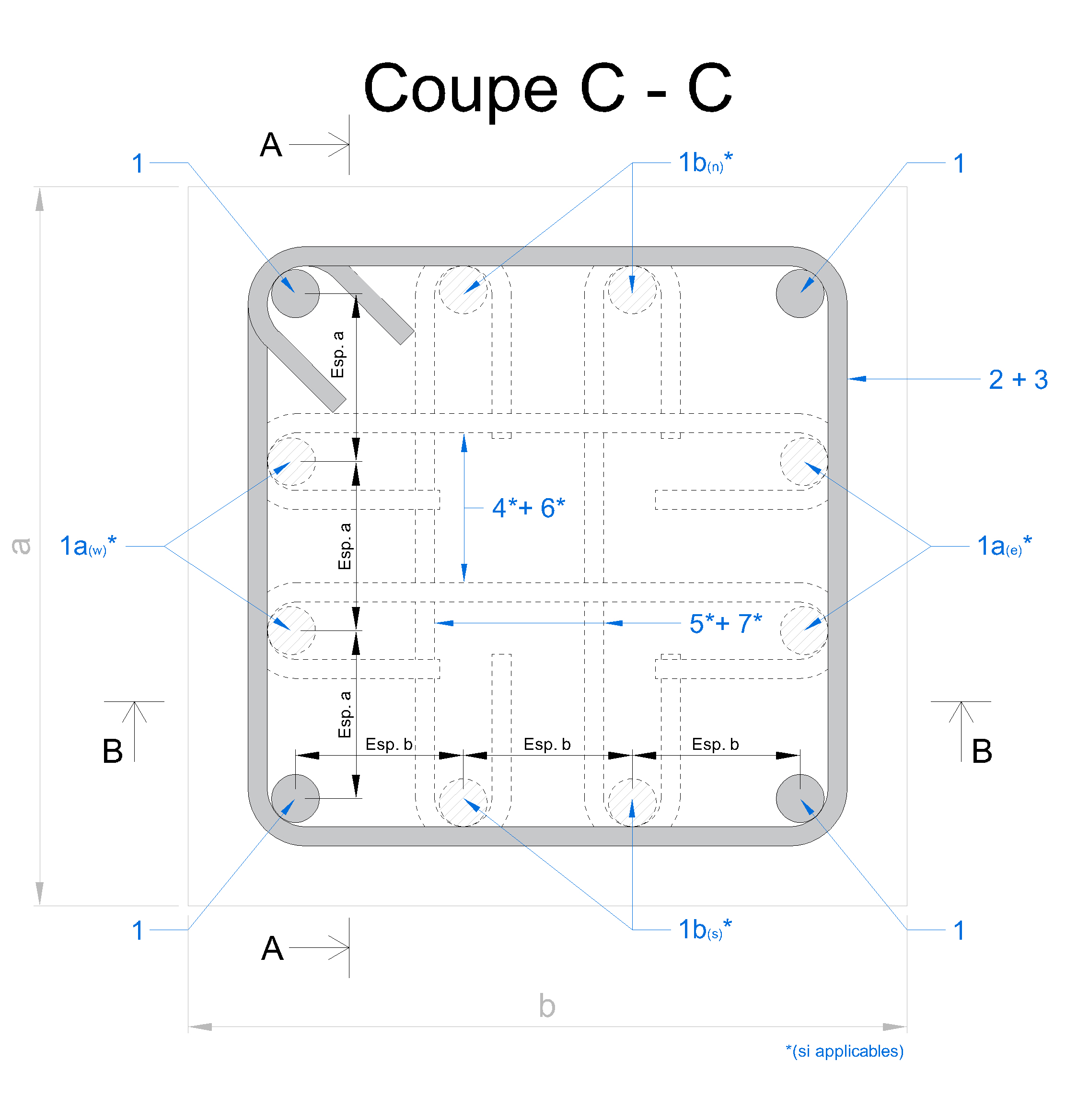
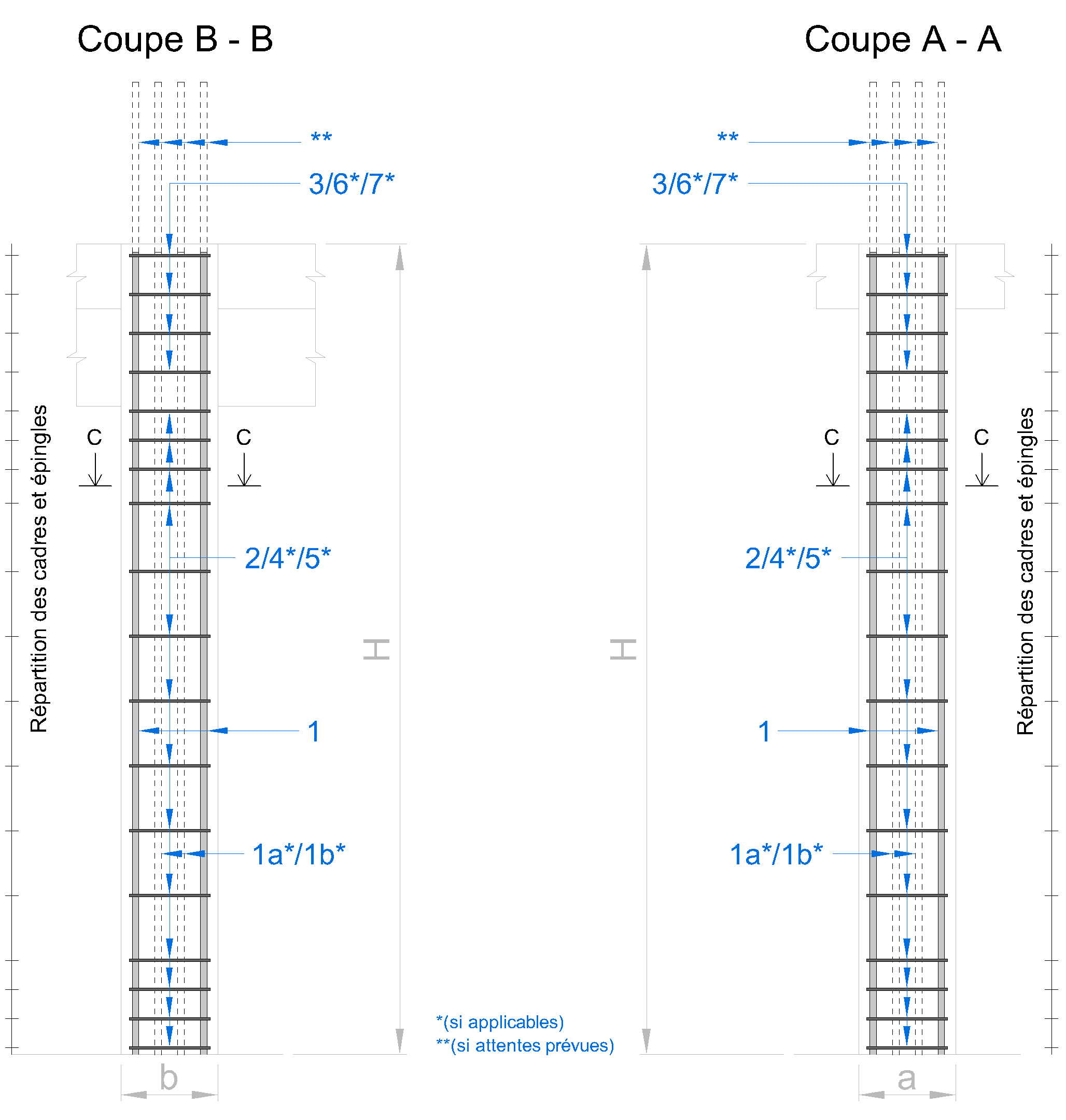
| Élément | Valeur | Unité |
|---|---|---|
|
Volume de béton (calculé sur hauteur nette dalle inf. → sous‑face poutre sup.) |
0.312 | m³ |
| Masse de béton | 748.8 | kg |
| Masse d’acier | 36.1 | kg |
| Masse totale (béton + acier) | 784.9 | kg |
| Ratio acier/béton | 4.82 | % |
| Longueur totale d’armatures | 43.59 | m |
| Diamètre moyen d'acier | 14 | mm |
Les résultats, schémas et tableaux de calcul présentés ci-dessus constituent une base claire et structurée pour le dimensionnement, la vérification et le ferraillage des poteaux en béton armé conformément à l’Eurocode 2. Cet outil en ligne a été conçu pour offrir à la fois clarté, précision et transparence, afin de faciliter la compréhension des principes de calcul et leur application pratique dans la conception des structures.
Il est essentiel de rappeler que toutes les valeurs obtenues doivent être contrôlées et validées par un bureau d’études qualifié avant toute application sur chantier. L’outil ne remplace pas le jugement de l’ingénieur, mais le complète : il fournit un cadre reproductible, traçable et conforme aux normes européennes, idéal pour la formation, la vérification rapide ou la préparation de notes de calcul.
Distribué sous licence libre et open source, ce logiciel encourage la collaboration, l’auditabilité et l’évolution continue du code. Cette démarche vise à démocratiser l’accès aux méthodes normalisées du calcul structurel et à favoriser une ingénierie plus transparente et interopérable. Les contributions et retours des utilisateurs sont vivement encouragés : toute suggestion d’amélioration, correction ou idée d’évolution peut être transmise via la page Contactez-nous ou directement sur le dépôt GitHub du projet.
Une fonction d’exportation automatique au format PDF sera prochainement intégrée, afin de permettre l’archivage et le partage des résultats dans vos processus de conception numérique (BIM, DAO, documentation technique, etc.).
Merci de votre confiance — nous espérons que ce calculateur libre vous accompagnera efficacement dans vos projets de conception et de dimensionnement de poteaux en béton armé.